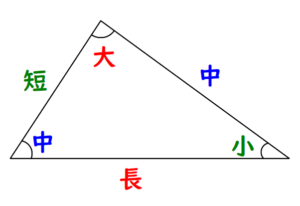
問題はこちら(画像をクリックするとPDFファイルで開きます。)
シンプルな3辺の長さをもつ三角形の内角がどの程度の大きさなのかを見積もる問題です。
具体的な値が出てこないことに対する恐怖感を拭えない受験生は多く、本問はキッチリと差がつく標準問題でしょう。
それにしても
\(\angle \mathrm{A}\)
という記号が不等号記号と一緒にされると見づらくてしょうがありません。
以下では単純に頂点 \(\mathrm{A}\) を見込む内角を単に \(A\) などと表すことにします。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む もちろん内角 \(B\) は具体的に口で言える角度ではありません。 裸の角度に対して我々ができることはほとんどなく、 という手段をとることになります。 3辺が分かっている状態では \(\cos{ \ }\) の服を着せるのが常套手段です。 余弦定理から $$\begin{eqnarray} となりますから、この値と \(\cos{45^{\circ}}\) , \(\cos{60^{\circ}}\) の値を比較します。 \(0^{\circ} \lt \theta \lt 180^{\circ}\) において、\(\cos{\theta}\) は単調減少なので \(\cos{60^{\circ}} \lt \cos{B} \lt \cos{45^{\circ}}\) を目指すことになります。 これも裸の角度のまま扱うことは躊躇われます。 今回は \(\cos{A}=\cos{2C}\) と、示すべき目標に \(\cos{ \ }\) の服を着せて言い換えます。 もちろん余弦定理を用いれば $$\begin{eqnarray} $$\begin{eqnarray} と、\(\cos{A}\) , \(\cos{C}\) の情報は手元に来ます。 これを基に \(\cos{2C}\) を 2 倍角の公式を用いれば \begin{eqnarray} と計算できるため、目標である \(\cos{A}=\cos{2C}\) が言えました。 なお、幾何的に示すこともできます。 それについては【解2】で紹介しています。 単純に \(\cos{ \ }\) の服を着せるのには限界があります。 もちろん、その理由は \(\cos{40^{\circ}}\) の値が口で言えないからです。 自分が解いた解き方は少々遠回りでした。 ひとまず (2) の結果から \(C=\theta\) とおけば、その他の連中も \(\theta\) で表せるじゃん。 と思い、 と設定しました。 そこから \(\theta\) についての不等式が得られるかなということで、先に思いついたのは \(C \lt B \lt A\) という角の大小関係です。 これは というように 基本事項
三角形の内角の大小と、対辺の長さの大小はリンクする という基本事項によります。 これを用いると \(\theta \lt 180^{\circ}-3\theta \lt 2\theta\) という不等式を得ます。 左側の不等式からは、目標の一つである \(\theta \lt 45^{\circ}\) が得られます。 ただ、右側の不等式からは \(\theta \gt 36^{\circ}\) が得られ、本来示すべき \(\theta \gt 40^{\circ}\) よりも甘い結果となってしまいます。 ここからのリカバリーですが、失敗した原因に注目します。 今回示すべき内容の結果と (2) から ということが言えます。 \(B \lt A\) という不等式を用いて失敗してしまったわけです。 この不等式の精度を上げるためにはよりシビアな角度で \(B\) を上から押さえる必要があるわけです。 そういった視点でふと見てみると と気がつくと思います。 \(B \lt 60^{\circ}\) ですから \(180^{\circ}-3\theta \lt 60^{\circ}\) すなわち \(\theta \gt 40^{\circ}\) を得ることができ、解決です。 もちろん、こんな右往左往しなくても最短距離で (1) の結果をフル活用して速攻で解決したという人もいるでしょう。 ただ遠回りをしてしまったこの解法についても、リカバリーの経緯などが参考になるかと思い公開しました。(1) について
\cos{B} &=& \displaystyle \frac{4^{2}+6^{2}-5^{2}}{2 \cdot 4 \cdot 6} \\
&=& \displaystyle \frac{9}{16}
\end{eqnarray}$$(2) について
\cos{A} &=& \displaystyle \frac{5^{2}+4^{2}-6^{2}}{2 \cdot 5 \cdot 4} \\
&=& \displaystyle \frac{1}{8}
\end{eqnarray}$$
\cos{C} &=& \displaystyle \frac{6^{2}+5^{2}-4^{2}}{2 \cdot 6 \cdot 5} \\
&=& \displaystyle \frac{3}{4}
\end{eqnarray}$$
\cos{2C} &=& 2\cos^{2}{C}-1 \\
&=& 2 \cdot \displaystyle \frac{3}{4}-1 \\
&=& \displaystyle \frac{1}{8}
\end{eqnarray}(3) について