例題はこちら(画像をクリックするとPDFファイルで開きます。)
離散量の不動点定理と呼ばれる有名な話題を扱います。
計算自体はほとんどありません。
構造を見抜く目と、それを記述しまとめる力が求められます。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む まず、問題文で何を言っているのかということをしっかりと把握します。 \(f\) という関数(写像)は「対応」という言葉で読み替えるとシックリくると思います。 イメージ的には というように、 という感じです。 \(f(k)=r\) というのは \(k\) の対応先が \(r\) と読むわけです。 ここで、\(f\) が広義単調増加であるという本問の条件を加味すると というように、\(\downarrow\) 方向の対応、または \(\searrow\) 方向の対応しかないということです。 今回は \(f(m)=m\) という不動点の存在を証明したい わけですが、 というように、 ということになります。 先述の 頑張っても最後には行き先がなくなる という構造を記述でまとめるには、背理法が大きな武器となります。 頑張っても最後には矛盾してしまう というオチで仕留める未来を見据えてまとめていきます。 構造を紐解いていくと、今回の離散量の不動点定理が元になっていることが分かります。 論証要素の純度が高く、処理力に重きを置きがちな東大にしては珍しいという点と、結果のインパクトから当時話題となった問題でもあります。 結構色々な問題集にも採用されています。 合否に影響があるかというと、恐らく影響はないでしょうが、腕を磨くにはいい題材です。題意を噛み砕く
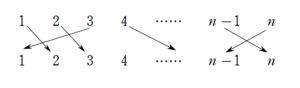
(上の例だと、\(2\) に対応:\(f(1)=2\))
(上の例だと、\(3\) に対応:\(f(2)=3\))
(上の例だと、\(1\) に対応:\(f(3)=1\))条件を加味すると
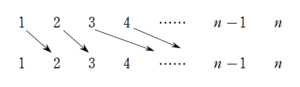
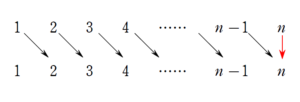
イメージを記述でまとめるには
応用例について
応用例はこちら(画像をクリックするとPDFファイルで開きます。)


