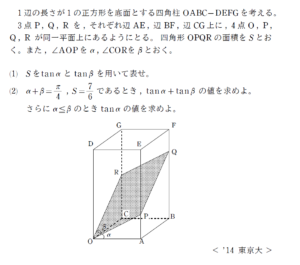
(1) について
この四角形 \(\mathrm{OPQR}\) が平行四辺形であることを看破したいところです。
断りなく平行四辺形と断定するかどうかについては、もちろん記述した方が望ましいに決まっています。
ただ実際には時間との兼ね合いもあるでしょう。
座標系を設定すれば割とスムーズに話が進みます。
(2) について
(1) で正しい結論が得られれば
\(S=\sqrt{1+\tan^{2}{\alpha}+\tan^{2}{\beta}}\)
と得られているはずです。
条件 \(S=\displaystyle \frac{7}{6}\) から
\(1+\tan^{2}{\alpha}+\tan^{2}{\beta}=\displaystyle \frac{49}{36}\)
を得ます。
残る \(\alpha+\beta=\displaystyle \frac{\pi}{4}\) という条件を、いかに使うかで明暗が分かれます。
方針1
\(\tan{(\alpha+\beta)}=1\)
と見ると、加法定理から
\(\displaystyle \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}}\)
を得るため、
\(\tan{\alpha}+\tan{\beta}\) , \(\tan{\alpha}\tan{\beta}=1\)
という等式が得られます。
つまり、先ほどの
\(1+\tan^{2}{\alpha}+\tan^{2}{\beta}=\displaystyle \frac{49}{36}\)
と併せれば、
\(\tan{\alpha}+\tan{\beta}\) , \(tan{\alpha}\tan{\beta}\)
という和と積に関する情報が得られます。
和は今回求めるものの一つですし、個別に求める \(\tan{\alpha}\) についても、和と積を活かした
解と係数の関係
で仕留めることも定番の内容です。
方針2
\(\alpha+\beta=\displaystyle \frac{\pi}{4}\) から、
\(\beta=\displaystyle \frac{\pi}{4}-\alpha\)
などと、1文字消去という路線も愚直な方針に見えます。
(1) 、及び条件 \(S=\displaystyle \frac{7}{6}\) から得られる
\(1+\tan^{2}{\alpha}+\tan^{2}{\beta}=\displaystyle \frac{49}{36}\)
に、\(\beta=\displaystyle \frac{\pi}{4}-\alpha\) を代入することで、\(\tan{\alpha}\) のみの4次方程式に帰着します。
\(\tan{\alpha}=T\)
などとおいて整理すると
\(36T^{4}+72T^{3}++59T^{2}-98T+23=0\)
という鬼4次方程式と遭遇します。
最高次の \(36\) の約数が多いため、心が折れるでしょう。
因数分解すれば
\((2T-1)(3T-1)(6T^{2}+17T+23)=0\)
となりますが、正直試験場だと相当焦る4次方程式で、あまり現実的とは言えない路線と言わざるを得ません。
まとめ
対称性を崩して、1文字消去するとトンデモ4次方程式が出てきてしまいました。
まぁ対称性に逆らうとロクなことはないのですが、それにしてもここまで顕著なのも驚きでしょう。
解答はコチラ