問題はこちら(画像をクリックするとPDFファイルで開きます。)
シンプルな問題です。
本問は試験場においては確保したいレベルの問題なのですが、確保するにしても手際の良さがわかれる要素を含んでいます。
本問を通じて持って帰りたい教訓は2点ほどあります。
(以下ネタバレ注意)
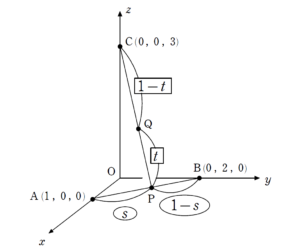
+ クリック(タップ)して続きを読む 与えられたシチュエーションを図示すると のような状況となります。 多分、この絵をかくときに、 \(P\) をまずかいて、その次に \(Q\) をかく という順番でかくと思います。 それは立式の順番にも反映され \(\overrightarrow{ OP }\) を求めて、その次に \(\overrightarrow{ OQ }\) を求める という順に求めることになります。 具体的には と立式して求めればよいでしょう。 計算過程は【解答】できっちりやりますが、 $$\overrightarrow{ OQ }=\left( となります。 結局 \(|\overrightarrow{ OQ }|^{2}\) の最小を考えればよく、 \(|\overrightarrow{ OQ }|^{2}=(1-t)^{2}(1-s)^{2}+4s^{2}(1-t)^{2}+9t^{2}\) の最小を考えることになります。 この式は \(s\) , \(t\) の独立 2 変数関数です。 独立 2 変数関数の最大最小を考えるにあたっての有力方針は 予選決勝法 です。 そこで、\(s\) , \(t\) のうち、どちらか一方を固定し、1文字ずつ動かしていくわけです。 さて、どちらを固定し、どちらを動かしますか? ここの判断をミスすると、本問は計算量がかなり変わってきます。 このあたりは見通しをもって選択できるようにしましょう。 これが上述した本問を通じた教訓の1つ目です。 ということはよくあります。 式的アプローチと図形的アプローチの判断については、普段から式と図形をリンクさせようとしているかという視点をもって勉強をしているかにかかってくるものです。 本問はもちろん予選決勝法を「式」で処理します。 その際、 自分が式で処理していることを「図形的なイメージをもちながら進める」 ということも大切なことです。 本問は式と図形的イメージを相互横断的にリンクさせる訓練として適度なレベルです。 本問でやった「処理」の図形的イメージについて【総括】でふれてあります。 このあたりが本問の教訓の2つ目です。状況を図示すると
\begin{array}{c}
(1-t)(1-s) \\
2s(1-t) \\
3t
\end{array}
\right)$$(2) について
図形的には

