例題はこちら(画像をクリックするとPDFファイルで開きます。)

2次方程式の解に関して注文が入る「解の配置問題」と呼ばれる問題です。
その中でも今回扱うのは
「少なくとも1つ」
というタイプです。
このタイプは手際が悪いとグチャグチャになる可能性が高いので、整理しながら集中して処理する必要があります。
王道的な態度に加え、こういう切り口から考えるのはどうだろうかという提案も込めて複数解法を紹介します。
とは言え、一度は自分の頭で考えて苦労しないと、工夫のありがたみ的な部分が薄れると思います。
自分で整理する際に、参考にしてくれればと思います。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
王道的な態度
与えられた2次方程式をそのまま
\(x^{2}-2ax+b=0\)
と見て、\(f(x)=x^{2}-2ax+b\) とおきます。
2次方程式の解をグラフの交点の \(x\) 座標と捉えて
\(y=f(x)\) と \(y=0\) ( \(x\) 軸 ) のグラフが \(0 \leq x \leq 1\) の範囲に少なくとも1つ交点をもつための条件
を考えるわけです。
分類
場合分けの分類としては
- \(0 \leq x \leq 1\) の範囲に重解を含めて2つの解をもつ
- 一方の解が \(0 \leq x \leq 1\) , 他方の解が \(x \leq 0\) または \(1 \leq x\) の範囲で解をもつ
という分類が王道的です。
提案
\(=0\) という方程式を相手にしなければならない理由はありません。
方程式の解をグラフの交点と捉えて、視覚的に処理する方針でいくのであれば
方程式の左辺と右辺を組み替えて、自分にとって考えやすいグラフで考える
という工夫も突拍子のない発想ではないでしょう。
ここでは \(x^{2}-2ax+b=0\) という方程式を
\(-x^{2}+2ax=b\)
と組み替えて、\(y=-x (x-2a)\) と、\(y=b\) のグラフが \(0 \leq x \leq 1\) の範囲で少なくとも 1 つ交点をもつための条件を考えていきます。
以下 \(f(x)=-x^{2}+2ax\) とします。
\(a \gt 0\) のとき
区間 \(0 \leq x \leq 1\) における \(1\) の場所で場合分けします。
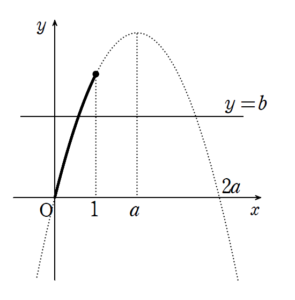
\(a \geq 1\) のとき

のような状況であるため、
\(0 \leq b \leq f(1)\)
となればよいことになります。
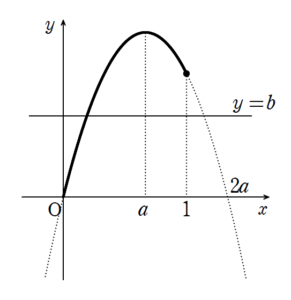
\(a \leq 1 \leq 2a\) , すなわち \(\displaystyle \frac{1}{2} \leq a \leq 1\) のとき

のような状況となるため、
\(0 \leq b \leq f(a)\)
となればよいことになります。
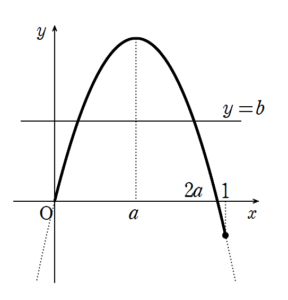
\(2a \leq 1\) , すなわち \(0 \lt a \leq \displaystyle \frac{1}{2}\) のとき

のような状況となるため
\(f(1) \leq b \leq f(a)\)
となればよいことになります。
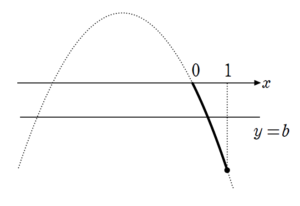
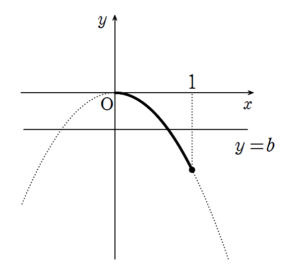
\(a \lt 0\) のとき

のような状況となるため
\(f(1) \leq b \leq 0\)
となればよいことになります。
特殊な \(a=0\) のときは

ですから、\(f(1) \leq b \leq 0\) となればいいわけです。
ただ、これは上の \(a \lt 0\) のときと同じ式で与えられるわけですから、まとめる際は
\(a \leq 0\) のとき
といった感じでまとめてしまえばよいでしょう。
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)

線分と放物線が共有点をもつための条件について考える問題ですが、紐解いていくと、結局は例題と同じ要領の問題に帰着します。
類題では
- 組み換えの工夫をした【解 1】
- \(=0\) のまま処理した【解 2】
に加えて、
を用意してあります。
例題の解答はコチラ
類題の解答はコチラ