問題はこちら(画像をクリックするとPDFファイルで開きます。)
複素数は
数値として扱えつつ、ベクトルとして幾何的にも扱える
という性質をもっているがゆえに、様々な解法が考えられる分野です。
多くの問題では \(z=x+yi\) などと「実部、虚部」を持ち出し、\(xy\) 平面の話に帰着させることで、慣れ親しんだ座標の話題に帰着させて考えても押し切れてしまいます。
複素数を複素数のまま扱うのか、実部、虚部を持ち出して処理するのかについては、この分野の方針決定上大きな路線選択です。
(以下ネタバレ注意)
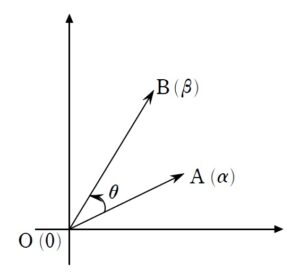
+ クリック(タップ)して続きを読む 反時計回りの向きを角度の正の向きとします。 \(A(\alpha)\) という複素数を原点の周りに \(\theta\) 回転& \(R\) 倍拡大(縮小)させてできる点を \(B(\beta)\) とします。 このとき、 原点中心の回転拡大 \(\beta=\alpha \cdot R(\cos{\theta}+i\sin{\theta})\) が成り立ち、複素数平面の旨味の一つである「回転作業」を表します。 もちろん、いつもいつも原点中心の回転とは限りません。 そこで、 \(A(\alpha)\) という複素数を \(P(z)\) の周りに \(\theta\) 回転& \(R\) 倍拡大(縮小)させてできる点を \(B(\beta)\) とします。 このとき、回転の中心 \(P(z)\) を原点に重ねるように平行移動させます。 すると、\(A'(\alpha-z)\) を原点の周りに \(\theta\) 回転& \(R\) 倍拡大(縮小)させてできる点が \(B'(\beta-z)\) ということになります。 なので P(z) 中心の回転拡大 \(\beta-z=(\alpha-z) \cdot R(\cos{\theta}+i\sin{\theta})\) ということが成り立ちます。 それぞれの複素数の値を「ベクトル的に見ると」 に対応します。 つまり、誤解を恐れずに言えば イメージ \(\overrightarrow{ PA }\) に「回転拡大パーツ」をかけたら(作用させたら)\(\overrightarrow{ PB }\) となった。 という風に捉えると、頭を整理しやすくなります。 何より、いちいち原点まで平行移動しなくてもパッと回転させられるでしょう。 (1) は回転の中心(引かれる複素数)が揃っていませんから \(\displaystyle \frac{z-\beta}{z-\alpha}\) を \(\displaystyle \frac{\beta-z}{\alpha-z}\) と見ます。 \(\beta-z=(\alpha-z)\cdot R(\cos{\theta}+i\sin{\theta})\) というように \(A(\alpha)\) という複素数を \(P(z)\) の周りに \(\theta\) 回転& \(R\) 倍拡大(縮小)させてできる点を \(B(\beta)\) としたときの式をイメージすれば \(\displaystyle \frac{\beta-z}{\alpha-z}\) という商は \(R(\cos{\theta}+i\sin{\theta})\) という「回転拡大パーツ」を意味するわけです。 この商の虚部が正となることを言えばいいわけです。 そうなってくると \(0 \lt \theta \lt \pi\) ということになるでしょう。 与えられた等式をどのように捌くかで方針が分かれます。 点 \(P\) が三角形 \(ABC\) の内部に存在するための条件は \(C\) が \(\overrightarrow{ PA }\) , \(\overrightarrow{ PB }\) で張られる斜交座標の「第3象限」に存在することです。 式的に言えば、 ベクトルで言えば \(\overrightarrow{ PC }=s\overrightarrow{ PA }+t\overrightarrow{ PB }\) と表したとき \(s \lt 0\) , \(t \lt 0\) ということになります。 今はベクトル風に言いましたが、複素数の言葉で言えば 複素数の言葉で言い直すと \(\gamma-z=s(\alpha-z)+t(\beta-z)\) と表したとき \(s \lt 0\) , \(t \lt 0\) ということになります。 そうなってくると与えられた等式については ひとまず \((z-\gamma)\) で括って \((z-\alpha) (z-\beta)+(z-\gamma)\{(z-\alpha)+(z-\beta)\}=0\) と見たくなるはずです。 ここから、目標に合わせて、\(\gamma-z\) を \(s(\alpha-z)+t(\beta-z)\) の形にしようという気持ちで式変形していけばよいでしょう。 (1) の形を活かそうと思えば、与えられた等式を両辺 \((z-\alpha)(z-\beta)\) で割りたくなります。 そうすることで \(1+\displaystyle \frac{z-\gamma}{z-\alpha}+\displaystyle \frac{z-\gamma}{z-\beta}=0\) と、(1) が活かせそうな形が現れます。 (1) は「虚部を見ろ」というメッセージですから両辺の虚部に注目すると \(Im(\displaystyle \frac{z-\gamma}{z-\alpha})+Im(\displaystyle \frac{z-\gamma}{z-\beta})=0\) ということになります。 (※ \(Im(w)\) とは \(w\) の虚部 ( Imaginary part ) を表します。) これが意味することは \(Im(\displaystyle \frac{z-\gamma}{z-\alpha})\) と \(Im(\displaystyle \frac{z-\gamma}{z-\beta})\) は異符号であるということです。 一方与えられた等式を \((z-\beta) (z-\gamma)\) で割って同様に虚部に注目すれば \(Im(\displaystyle \frac{z-\alpha}{z-\beta})\) と \(Im(\displaystyle \frac{z-\alpha}{z-\gamma})\) は異符号 ということが分かります。 先ほどの、 \(Im(\displaystyle \frac{z-\gamma}{z-\alpha})\) と \(Im(\displaystyle \frac{z-\gamma}{z-\beta})\) は異符号 と見比べると、微妙に分母分子が逆数になっています。 一般に、\(u+vi\) に対して \(\displaystyle \frac{1}{u+vi}=\displaystyle \frac{1}{u^{2}+v^{2}}(u-vi)\) ですから、逆数同士の虚部は異符号と言うことに注意して微調整をしていきましょう。 本問の背景には ガウス・ルーカスの定理 複素数平面上で \(f(z)=0\) に対応する点を \(A_{i}\) とする。 \(f'(z)=0\) に対応する点は \(A_{i}\) の凸包に含まれる という定理があります。 本問は \(f(z)=(z-\alpha)(z-\beta)(z-\gamma)\) としたときのガウス・ルーカスの定理そのものです。 もちろん、そんな事実を知っていようが前面に押し出すわけにはいかないので、全く影響はありません。複素数平面の回転について
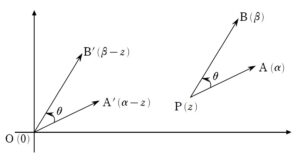
(1) の複素数の商について
(2) について
点 P が三角形ABCの内部に存在することの直訳
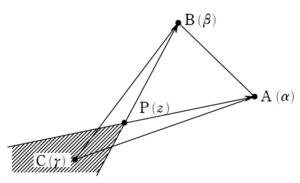
(1) を誘導と見れば
対称性を利用
本問の背景的な定理

