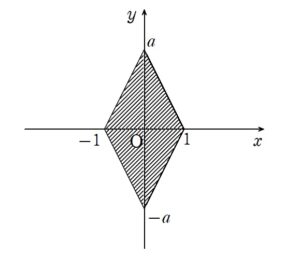
今回の領域を図示すると
今回与えられた不等式 \(a|x|+y \leq a\) を図示すると

というひし形の内部になります。
王道的な態度だと
線形計画法の考え方
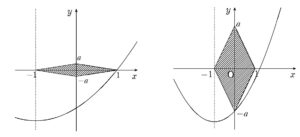
\(y-(x+1)^{2}=k\)
とおいて、
放物線 \(y=(x+1)^{2}+k\) が与えられた領域とぶつかるかどうかを考える
というアプローチが自然でしょう。
最小値について
今回動かす放物線は軸が \(x=-1\) で固定なので、単純に上下に動きます。
また、今回の領域を与える不等式に入っている \(a\) によって、平べったいひし形なのか、縦に細長いひし形なのかが分かりません。
それによって

というように
- \((1 \ , \ 0)\) を通るときが下げる限界
- \((0 \ , \ -a)\) を通るときが下げる限界
と場合分けが発生します。
最大値について
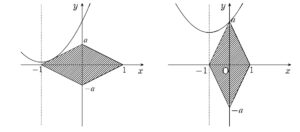
今度は放物線を「上げよう上げよう」という気持ちです。
ただし、やはりここでも

というような「上げ」の限界のケースについて場合分けが発生します。
特に左の図では
\(y=(x+1)^{2}+k\) と \(y=ax+a\) が接するときを考えるだけでなく、\(-1 \lt x \lt 0\) で接するという範囲付きであるため、嫌だなと思うでしょう。
スマートに処理
このように接するだの接さないだの、通るだの通らないだのといった
図形的観点からの場合分け
はめんどくさいと思います。
どうせ境界線上の \((x \ , \ y)\) で最大(最小)が起こる
初見の方はともかく、難関大受験生であれば、線形計画法に関する問題の一つや二つや三つや四つは当然解いていてマスターしているはずです。
線形計画法は \(=k\) とおいて、与えらえた領域とぶつかる中での
上げの限界(下げの限界)
を捉える考え方です。
限界ギリギリまで上げたり、下げたりするわけですから、当然最大最小を起こす \((x \ , \ y)\) は領域の境界線上の \((x \ , \ y)\) に決まっています。
本問の最大値で言うと

\(y=ax+a\) ( \(-1 \leq x \leq 0\) ) という線分上の \((x \ , \ y)\) で最大が起こり得ることになります。
そこで、この線分
\(y=ax+a\) ( \(-1 \leq x \leq 0\) )
上の点
\((t \ , \ at+a)\) ( \(-1 \leq t \leq 0\) )
について考えます。
\((x \ , \ y)=(t \ , \ at+a)\) ( \(-1 \leq t \leq 0\) ) としたときの \(k\) の値について考えればいいわけです。
\(k=y-(x+1)^{2}\) とおいていたわけでしたから、\(k=(at+a)-(t+1)^{2}\) , すなわち
\(k=-t^{2}+(a-2)t+a-1\)
の \(-1 \leq t \leq 0\) における最大値を考えればよく、ただの2次関数の最大値問題に帰着します。
このように境界線上のどの点で最大(最小)になるかを考える考え方は、煩雑な線形計画法の問題全般において有効で、割と守備範囲の広い考え方なのでぜひ自分のものとしてください。
解答はコチラ