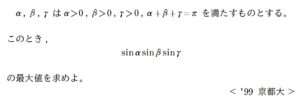問題はこちら(画像をクリックするとPDFファイルで開きます。)
シンプルな問題ですが、多くの解法が考えられ、それぞれ色々な教訓を含んでいるので、一粒で何度もおいしい問題です。
どういう視点からこの問題を捉えるかによって、自然に見える見え方や考え方が変わってきます。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 見た目通りの問題と捉えると この問題を見た目通り 「従属な3変数関数の最大問題」 と捉えれば、例えばまずは \(\gamma\) を消去して、\(\alpha\) , \(\beta\) のみの式とし、その後は \(\alpha\) , \(\beta\) の独立2変数関数として考えます。 その処理は予選決勝法でしょう。 対称性が目につくと 「対称性を活かす路線」 という目線で捉えれば、絶対不等式の活用の一つとして、和と積に関する絶対不等式の代表選手である「相加平均・相乗平均の関係」が考えられます。 今回の角度を三角形の内角と見ると \(\alpha\) , \(\beta\) , \(\gamma\) が \(\alpha+\beta+\gamma=\pi\) を満たす正の角度ということから \(\alpha\) , \(\beta\) , \(\gamma\) は三角形の内角 と捉え、そこから「式のもつ意味を図形量として捉えよう」という気持ちを考えると幾何的に捉える路線も見えてきます。 もちろん、今述べた数々のものの見方は口で言うほど簡単ではないと思います。 どんな路線が自然に見えるのか? 見える人には何が見えているのか? 天才型ではない私自身が初学者だったとき、心がけていたことはまさにそこでした。 闇雲に何問も解きあさるのではなく、「何とかしよう」という意識を持ちながら続けていれば、徐々に景色が変わっていくはずです。 問題はこちら(画像をクリックするとPDFファイルで開きます。) 三角形の内角に関する不等式で、シンプルな題意です。 解法も様々考えられ、京大らしい問題だと思います。 試験場では愚直に解くのが現実的です ... 続きを見る 問題はこちら(画像をクリックするとPDFファイルで開きます。) 非常にシンプルな問題です。 切れ味鋭く捌くこともできますし、腕力で押し切ることもできます。 いずれの路線にせよ、確かな力が必要です。 類 ... 続きを見る 類題も適宜活用してください。類題

参考三角形の内角に関する不等式【cosα+cosβ+cosγ≧1】【2005年度 京都大学】

参考三角形の内角のtanの和【1966年度 金沢大学】