問題はこちら(画像をクリックするとPDFファイルで開きます。)

18°絡みの三角比という話題で、様々な切り口からこのテーマが扱われます。
代表的な登場シーンを一通り経験することで、ストーリーを体感し、対応できるようにしましょう。
このシリーズの一覧はこちら
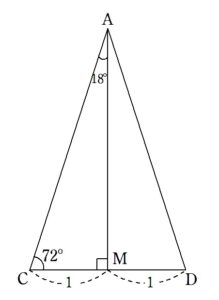
18°絡みの三角比 第1講【黄金三角形の黄金分割】【2009年度 大阪教育大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 18°絡みの三角比という話題で、様々な切り口からこのテーマが扱われます。 代表的な登場シーンを一通り経験することで、ストーリーを体感し、対応できるようにしましょう。 このシリーズの一覧はこちら 第1講は 黄金三角形の黄金分割 という話題です。 黄金比について 長方形 A から正方形を切り取って 残った長方形を B とします。 A と B が相似であるとき、長方形 A を黄金長方形といい、その縦横比を \(1 : x\) とすると、 \(1 : ...
続きを読む
18°絡みの三角比 第2講【正五角形の利用】【1997年度 岐阜大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 18°絡みの三角比という話題で、様々な切り口からこのテーマが扱われます。 代表的な登場シーンを一通り経験することで、ストーリーを体感し、対応できるようにしましょう。 このシリーズの一覧はこちら 第2講は 正五角形の利用 という話題です。 正五角形はゴールドラッシュ 正五角形の中には第1講で扱った「黄金三角形」が至る所に散りばめられています。 まさに「ゴールドラッシュ」な状態です。 黄金三角形については第1講 で扱っ ...
続きを読む
18°絡みの三角比 第3講【チェビシェフの多項式の利用】【2012年度 早稲田大学ほか】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 18°絡みの三角比という話題で、様々な切り口からこのテーマが扱われます。 代表的な登場シーンを一通り経験することで、ストーリーを体感し、対応できるようにしましょう。 このシリーズの一覧はこちら 第3講は チェビシェフの多項式の利用 という話題です。 通常の流れ 通常の例題 \(\theta\) が \(0 \leq \theta \leq \pi\) を満たしているとき \(2\cos^{2}{\theta}+\c ...
続きを読む
18°絡みの三角比 第4講【1の5乗根の利用】【1997年度 金沢大学ほか】
例題はこちら(画像をクリックするとPDFファイルで開きます。) 18°絡みの三角比という話題で、様々な切り口からこのテーマが扱われます。 代表的な登場シーンを一通り経験することで、ストーリーを体感し、対応できるようにしましょう。 このシリーズの一覧はこちら 第4講は 1の5乗根の利用 という話題です。 複素数平面と三角関数の強力なコラボレーションが心地よく感じると思います。 (以下ネタバレ注意) + クリック(タップ)して続きを読む 最終的なオチ 三角関数を扱ううえで、複素数平 ...
続きを読む
第2講は
正五角形の利用
という話題です。
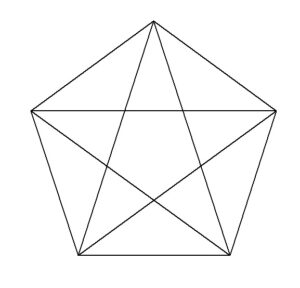
正五角形はゴールドラッシュ

正五角形の中には第1講で扱った「黄金三角形」が至る所に散りばめられています。
まさに「ゴールドラッシュ」な状態です。
黄金三角形については第1講
-

-
黄金三角形18°絡みの三角比 第1講【黄金三角形の黄金分割】【2009年度 大阪教育大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 18°絡みの三角比という話題で、様々な切り口からこのテーマが扱われます。 代表的な登場シーンを一通り経験することで、ストーリーを体感し、 ...
続きを見る
で扱っています。
(1) について

という黄金三角形の黄金分割を利用してやることが考えられます。
(2) について
第1講同様、黄金三角形を真っ二つにしてやればよいでしょう。

として、\(\displaystyle \frac{CM}{AC}\) などと見てやります。
(3) について
どのように分割するかですが
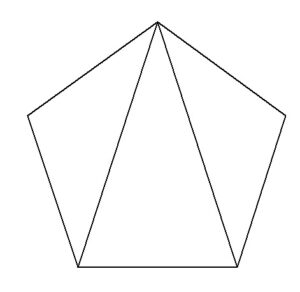
路線1

というように鈍角の黄金三角形2つと、鋭角の黄金三角形に分割するという方法が考えられます。
あるいは
路線2

というように、この正五角形の各頂点と中心と結んでできる二等辺三角形5つ分の面積を計算する路線も考えられます。
どちらが先に目に付くかは個人差があるでしょうが、外れない二重根号が登場するので、いずれにせよ目に付いた路線で計算を進めるうえでは集中力がいります。
解答はコチラ