問題はこちら(画像をクリックするとPDFファイルで開きます。)
18°絡みの三角比という話題で、様々な切り口からこのテーマが扱われます。
代表的な登場シーンを一通り経験することで、ストーリーを体感し、対応できるようにしましょう。
このシリーズの一覧はこちら
第1講は
黄金三角形の黄金分割
という話題です。
黄金比について
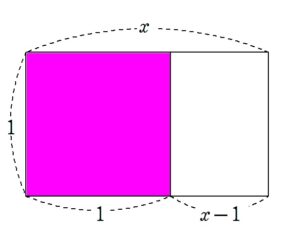
長方形 A から正方形を切り取って 残った長方形を B とします。
A と B が相似であるとき、長方形 A を黄金長方形といい、その縦横比を \(1 : x\) とすると、
\(1 : x=x-1 : 1\)
これを整理した \(x^2-x-1=0\) の正の解として \(x=\displaystyle \frac{1+\sqrt{5}}{2}\) が得られますが、この値を
\(\phi=\displaystyle \frac{1+\sqrt{5}}{2}\)
と、\(\phi\) という文字で表し、これを黄金数(あるいは分数自体が比を表すことから黄金比)と呼びます。
古来より人類が最も美しく感じる比率として、ミロのヴィーナスやパルテノン神殿など、様々な文化財に取り入れられています。
黄金三角形について
今回取り上げられている三角形は
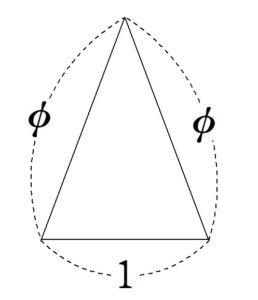
という辺の比が \(\phi : 1\) となっている二等辺三角形です。
この \(\phi\) は元々\(1 : x=x-1 : 1\) を満たす \(x\) として得られた値ですから、当然
\(1 : \phi=\phi-1 : 1\)
を満たしています。
したがって
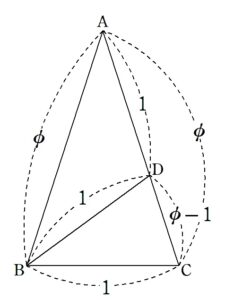
という分割によって \(\triangle ABC ∽ \triangle BCD\)という相似構造が現れます。
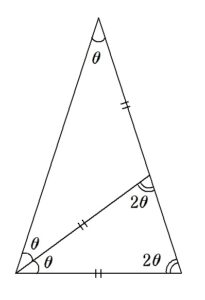
と角度 \(\theta\) を設定すると、\(5\theta=180^{\circ}\) より、\(\theta=36^{\circ}\) を得ることになります。
本問について
本問で与えられている二等辺三角形は黄金三角形です。
一応誤解がないように言っておきますが、\(36^{\circ}\) , \(72^{\circ}\) , \(72^{\circ}\) の二等辺三角形だから黄金三角形というよりも
黄金三角形は
結果的に\(36^{\circ}\) , \(72^{\circ}\) , \(72^{\circ}\) の二等辺三角形となっている
というニュアンスです。
本問の話題としては (2) の \(\cos{72^{\circ}}\) の導出ですが、この黄金三角形を真っ二つにすることで
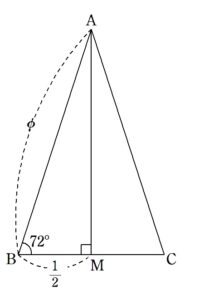
と見て、\(\cos{72^{\circ}}=\displaystyle \frac{BM}{AB}\) として導出できることになります。
(3) は、黄金分割を活かした設問で、典型的な話題というわけではありませんが、対応力や活用力、幾何の総合力を試す実戦的な良問です。





