問題はこちら（画像をクリックするとPDFファイルで開きます。）
今回の話題は
\(\displaystyle\frac{1}{n}\)乗の対数の極限
です。
昔
\(\displaystyle\frac{1}{3}\) の純情な感情
という曲がありました。
響きが似ていますね。
これが言いたかっただけです。
今回の話題は個人的に壊れるほど愛しているのですが、\(\displaystyle\frac{1}{3}\) も伝わればいいなと思います。
今のくだりが \(\displaystyle\frac{1}{3}\) も伝わらなかった方は原曲を聞いてください。
（以下ネタバレ注意）
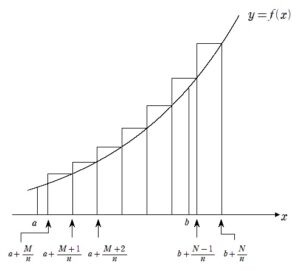
+ クリック（タップ）して続きを読む 教科書には 区分求積法の式 \(\displaystyle \lim_{ n \to \infty } \displaystyle\frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle\frac{k}{n}) = \displaystyle \int_{0}^{1} f(x) dx\) という区分求積法の公式があります。 教科書には積分区間が 0 から 1 までのものが載っていますが、 一般の積分区間での区分求積法の式 \(\displaystyle \lim_{ n \to \infty } \displaystyle\frac{1}{n}\displaystyle \sum_{k=an+M}^{bn+N} f(\displaystyle\frac{k}{n}) = \displaystyle \int_{a}^{b} f(x) dx\) という積分区間が \(a\) から \(b\) までのものについてもきちんと準備しておきましょう。 実戦的にはシグマの区間の \(n\) の係数とリンクしていますから、手際よく処理すればよいですが、もちろん という図形的なイメージもきちんと押さえておきたいですね。 さて、本問についてですが、誘導があるために、\(\log\) を取ろうという気になると思います。 基本的に \(P_{n}=( \ \ \ \ )^{\frac{1}{n}}\) という形に対して \(\log P_{n}=\displaystyle\frac{1}{n}\log \sum_{ \ }^{ \ }\) という形になるため、\(\displaystyle\frac{1}{n}\) 乗の部分が将来の区分求積法におけるパーツとなります。 一連の流れとシナリオについてはきちんと理解して、誘導に期待することなく解ききってほしいと思います。 実際北海道大学では誘導がありましたが、横浜国立大学の方は(2)単独での出題です。 そのために「くどい」と思うぐらいの類題を用意してますので、適宜ご活用ください。
（本来これも深い内容を含む話題ですが、それはまた別の機会に）