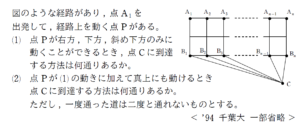
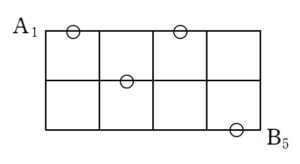
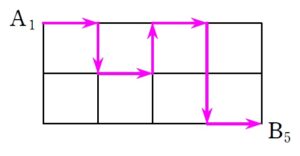
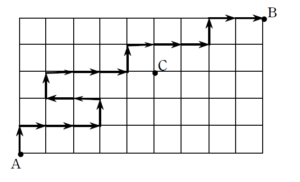
例題はこちら(画像をクリックするとPDFファイルで開きます。)
定番の経路問題をベースとして、プラスアルファの思考要素が入った問題です。
(1) は落としたくないレベルですが、(2) は難問です。
東大に現役で合格するような受験生でも、このタイプは初見だと四苦八苦します。
逆に、割合は少ないですが、あっさりと解決してしまう人もいるので見える人には見えるのでしょう。
なお、(2) のモデルケースを考えてみると、蛇みたいな経路に見えるので、蛇経路と呼んでいます。
(私が勝手に呼んでいるだけで市民権はありません。)
(以下ネタバレ注意)