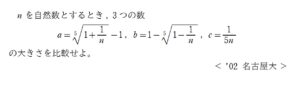問題はこちら(画像をクリックするとPDFファイルで開きます。)
5乗根に関する数の大小比較の問題です。
目に付いた特徴によって様々な解法が考えられるあたりが面白いところです。
結論自体に辿り着くことは決して難しくはないので、色々考えてみてほしいと思います。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む あたりをつけるために、\(n=1\) としてみると \(a=\sqrt[5]{2}-1\) , \(b=1\) , \(c=\displaystyle \frac{1}{5}\) です。 \(a\) , \(c\) は \(1\) より小さいため、最大は \(b\) だと予想がつきます。 残る \(a\) , \(c\) の比較については、 \(a+1=\sqrt[5]{2}\) と \(c+1=\displaystyle \frac{6}{5}\) の大小を比較すればよく \(2\) と \((\displaystyle \frac{6}{5})^{5}\) の比較をすればよいでしょう。 ここの算数については若干歯を食いしばって計算すると \(2 \lt (\displaystyle \frac{6}{5})^{5}\) と言えます。 このことから \(a \lt c \lt b\) という予想が立ちます。 あとはこの予想を裏付ける証明をしていきます。 \(a \lt c\) \(\Leftrightarrow\) \(\sqrt[5]{1+\displaystyle \frac{1}{n}}-1 \lt \displaystyle \frac{1}{5n}\) \(\Leftrightarrow\) \(\sqrt[5]{1+\displaystyle \frac{1}{n}} \lt 1+\displaystyle \frac{1}{5n}\) \(\Leftrightarrow\) \(1+\displaystyle \frac{1}{n} \lt (1+\displaystyle \frac{1}{5n})^{5}\) と示すべきことをほぐしていきます。 こうしてみると、右辺を5乗展開したときに、左辺の \(1+\displaystyle \frac{1}{n}\) が現れますから、この示すべきターゲットは二項定理による展開で沈むことになります。 \(c \lt b\) についての証明も同様に、示すべきことをほぐしていきましょう。 この路線は【解1】で扱っています。 与えられた5乗根は目がチカチカする形です。 そこで、 と、おいてしまいます。 これにより となりますが、 という因数分解が目につきます。 ここから $$\begin{eqnarray} となり、 \(p-1 \lt \displaystyle \frac{1}{5n}\) すなわち \(a \lt c\) を得ます。 \(c \lt b\) についても同様です。 この路線は【解2】で扱っています。 累乗根がからむ不等式証明として、相加平均・相乗平均の関係を用いると、まるでウソのように沈みます。 5乗根が絡んでいるため、5数の相加平均・相乗平均の関係を考えていきます。 という5数に対して相加平均・相乗平均の関係から \(1+1+1+1+(1+\displaystyle \frac{1}{n}) \geq 5\sqrt[5]{1\cdot 1\cdot 1\cdot 1\cdot (1+\displaystyle \frac{1}{n})}\) すなわち \(5+\displaystyle \frac{1}{n} \geq 5 \sqrt[5]{1+\displaystyle \frac{1}{n}}\) を得ます。 等号成立は \(1=1+\displaystyle \frac{1}{n}\) のときですが、これはあり得ないため、等号は成り立ちません。 よって \(1+\displaystyle \frac{1}{5n} \gt \sqrt[5]{1+\displaystyle \frac{1}{n}}\) となり、\(a \lt c\) を得ます。 \(c \lt b\) の証明については、 という5数について、同様に相加平均・相乗平均の関係を用いれば示すことができます。 この路線は【解3】で扱っています。結論の予想
路線1:示すべきことをほぐしていく
路線2:累乗根の部分を置き換える
\displaystyle \frac{1}{n}&=& (p-1)(p^{4}+p^{3}+p^{2}+p+1) \\
& \lt & (p-1)(1+1+1+1+1)\\
&=& 5(p-1)
\end{eqnarray}$$路線3:相加平均・相乗平均の関係の利用