問題はこちら（画像をクリックするとPDFファイルで開きます。）
図形を折るこの手の問題は想像力が必要で、中学受験を経験している中高一貫校の生徒は割とそういう訓練を積んでいる人が多いです。
それがいいか悪いかはおいておきます。
見え方が鋭い人はそれを活かせばいいと思いますし、急所に辿り着くのに時間がかかるという人は多少時間がかかっても地に足つけて解ければいいと思います。
ただ、見える人には何が見えているのかということを意識しながら勉強していくことが大切です。
本問は見える人にはパッと見えるのでしょう。
戦略、解答は地道に（丁寧に）前進していく感じの解答です。
ただ、幾何特有の
「言葉にしにくい」
という部分が大いにあると思います。
（以下ネタバレ注意）
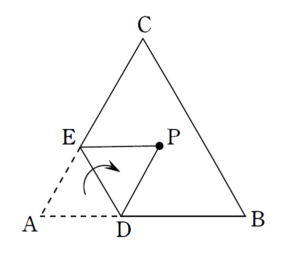
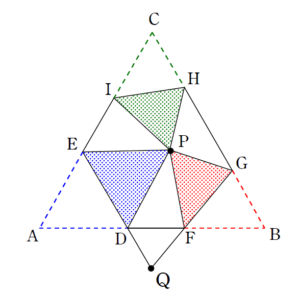
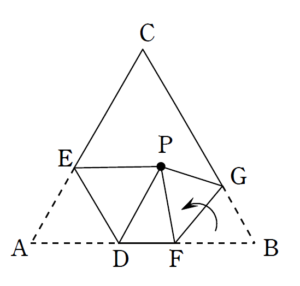
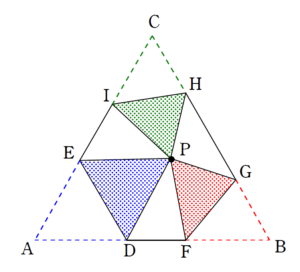
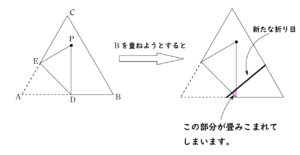
+ クリック（タップ）して続きを読む いきなり考えるのではなく、一つずつ重ねてみましょう。 頂点 \(A\) を \(P\) に重ねてみます。 この段階では何かが掴めるというわけではないと思います。 とりあえず、 折り目は線分 \(AP\) の垂直二等分線 ということは見えやすいでしょうか。 次に \(B\) を \(P\) に重ねてみます。 このあたりから、「６辺形」の片鱗が見え始めてきます。 この勢いで \(C\) も重ねてみます。 すると というようになります。 分かることとしては 六角形を構成する辺としては という構造です。 確かに六角形ができましたが、これで点 \(P\) の場所の制約に迫れるかというと疑問です。 そこで ダメなケースは？ という流れで頭が動くと、「\(P\) がどうあるべきか」というのが見えてきます。 \(P\) が変な位置にある場合を考えてみます。 六角形ができないとき 新たな折り目が「重なりの部分を巻き込んで」畳みこまれてしまう ということを想像したいところです。 このことから、 折り目同士が正三角形内で交わって巻き込まれてしまうとヤバい ということが言えます。 逆に、それを回避できれば題意の六角形ができるということになります。 折り目の直線の交点は 垂直二等分線同士の交点 です。 そうなると外心の議論になります。 例えば というように \(Q\) を定めると、\(Q\) は 線分 \(AP\) , \(BP\) の垂直二等分線の交点 ですから、\(\triangle ABP\) の外心です。 この外心 \(Q\) が三角形 \(ABP\) の外部にあるということなので、 \(\angle APB \gt \displaystyle \frac{\pi}{2}\) となっていればよいことになります。 このことから、点 \(P\) は 線分 \(AB\) を直径とする円の内部に存在する ということが言えます。 同様に考えると、点 \(P\) は 正三角形の各辺を直径とする円の内部 に存在すればよいことになります。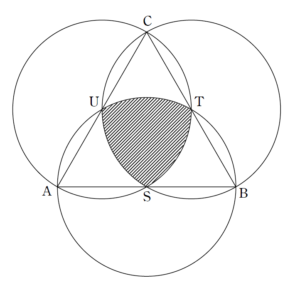 図示すると のようになります。 この図形は「ルーローの三角形」と呼ばれる有名な図形です。 面積計算自体は中学生でもできる範囲です。 こちらも良問 問題はこちら（画像をクリックするとPDFファイルで開きます。） 正方形の折り紙を折り曲げたときの重なりの部分が線対称な五角形になるときを考える幾何的な問題です。 このあたりの幾何的な考察はマニュアル的 ... 続きを見るとりあえず一つ重ねてみる
二つ目を重ねてみる
下手くそなＰだと
折り目の交点は
その他の折り紙問題の良問
正方形を折ったときの重なりの五角形【2001年度 東京工業大学】