問題はこちら(画像をクリックするとPDFファイルで開きます。)
方程式の解に関して、様々な考察をさせる良問です。
この年にこの問題を解いたとき、教材として使いたいなと思った記憶があります。
(以下ネタバレ注意)
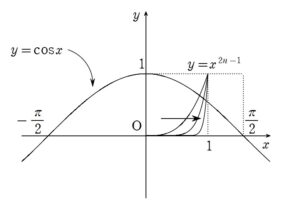
+ クリック(タップ)して続きを読む 意外と侮れません。 機械的に差を取って微分して \(\cdots\) という態度では、はじき返されるでしょう。 下手に移項せず、\(x^{2n-1}=\cos{x}\) のまま見て、\(y=x^{2n-1}\) , \(y=\cos{x}\) のグラフの交点について考えていきます。 明らかに交点をもたないであろう範囲をどんどん削っていく感じで話を組み立てていけばよいのですが、自分で話を組み立てるという経験がないとオロオロしかねません。 視覚化できれば、問題の主張はほぼ明らかです。 \(0 \lt a_{n} \lt 1 \lt \displaystyle \frac{\pi}{2}\) であることに注意すれば、その範囲で \(y=\cos{x}\) が単調減少であることを丁寧に記述すればよいでしょう。 のように視覚化して考えると交点の \(x\) 座標はどんどん \(1\) に近づいていくため、\(\displaystyle \lim_{n \to \infty} a_{n}=1\) であることは予想できます。 (2) での考察で、\(a_{n} \lt 1\) と上から押さえられていることは分かっていますから、あとは下から押さえてはさみうちの原理で仕留める方向を見据えたいところです。 \(a_{n}\) は具体的な式で表されるわけではありませんから、はさみうちの原理で仕留める流れはきっちりと押さえておきましょう。 ココがポイント
本人不在の極限は、はさみうち \(\displaystyle \lim_{n \to \infty} a_{n}^{n}\) については、\(a_{n}^{2n-1}=\cos{a_{n}}\) という関係式から、無理やりにでも \(\displaystyle \lim_{n \to \infty} (a_{n}^{2n-1})^{\frac{n}{2n-1}}\) と見てやれば解決します。 \(c\) については頭を悩ませるかもしれませんが、\(\displaystyle \lim_{n \to \infty} \displaystyle \frac{a_{n}^{n}-\sqrt{\cos{1}}}{a_{n}-1}\) なので、 \(\displaystyle \frac{F(x)-F(1)}{x-1}\) という形で見れるような \(F(x)\) を見出すことができれば、「微分係数の定義」によって仕留めることができるでしょう。 総合的に見ると、「確かな力」が必要な問題です。 用いる手法自体はよくある定番のものですが、そうと判断するためには確かな経験に加え、洞察力を要します。(1) について
(2) について
(3) について