問題はこちら(画像をクリックするとPDFファイルで開きます。)
斜軸回転体の体積というテーマ性のある話題です。
通常の \(x\) 軸回転体、\(y\) 軸回転体に加え、マスターしておきたい話題のひとつでしょう。
斜軸回転体の試験場(記述式)での倒し方は次のいずれかです。
斜軸回転体の倒し方
①:回転軸に対して垂直に切り、変数変換(置換積分)
②:回転軸を回転させて \(x\) 軸に重ねる。
※ 傘型分割というイキった解法もありますが、順番的には① , ② をきちんとマスターすべきです。

① の方針について
今回は回転軸である \(y=x\) を変数軸として \(t\) 軸とします。
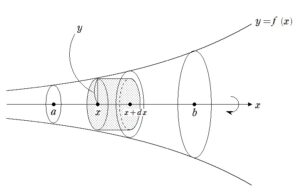
新たな座標軸において \(t=k\) と切ったとき、切り口の線分の長さを \(r_{k}\) とすると
\(V_{n}=\displaystyle\int_{0}^{\sqrt{2}} \pi r_{k}^{2} dk\)
ということになります。
しかし、この \(r_{k}\) が \(k\) の式で出ません。
というのも、\(x\)軸が水平軸の場合、曲線 \(C\) は \(y=x^{n}\) という直交座標表示で表されていますが、首をかしげて(首を45°傾けて)\(t\) 軸を水平軸に見たとき、曲線 \(C\) の式が変わってしまうからです。
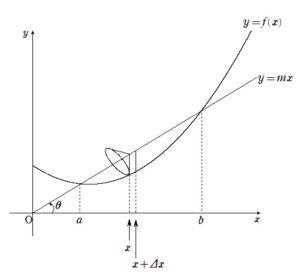
そこで、まずは図のように \(\alpha\) と設定します。
この \(r_{k}\) に相当する長さを「点と直線の距離」で仕留めることをインスピレーションすれば
\(r_{k}=\alpha\) の式
となりそうです。
この時点で最終的なシナリオは \(\alpha\) への変数変換(置換積分)です。
あとは \(dk\) を \(d\alpha\) に変える必要がありますから、\(k\) と \(\alpha\)との関係を求めに行くことになるでしょう。
② の方針について
先ほど、\(t\) 軸を水平軸に見たとき、曲線 \(C\) の式が変わってしまうと述べました。
逆に言えば首をかしげて見たときの曲線 \(C\) の式が Get できたのなら \(r_{k}\) に相当する長さが簡単に求まることを意味します。
そこで、\(t\) 軸を \(x\) 軸に重ねるように回転させます。
曲線 \(C\) 上の各点 \((u \ , \ u^{n})\) を \(-45^{\circ}\) 回転させるために
\((u+u^{n}i) ( \cos{(-45^{\circ})}+i\sin{(-45^{\circ}}) )\) を計算し、実部虚部を見れば、曲線 \(C\) を \(-45^{\circ}\) 回転させた曲線 \(C'\) のパラメータ表示が得られます。
パラメータ曲線さえ得られれば、あとは \(x\) 軸回転体に帰着します。
傘型分割について
以下は毒にも薬にもなる話ですから、隠させていただきます。