例題はこちら(画像をクリックするとPDFファイルで開きます。)
放物線と円の共有点の個数について直球で訊いている問題です。
放物線と円の共有点については結構ウルサイので、場当たり的になってしまうことも多いかと思います。
直感的に処理できる部分や、式に教えてもらう部分が混在するところもあるため、一つずつ丁寧に整理していきましょう。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む \(x^{2}+y^{2}=1\) と \(y=ax^{2}+b\) を連立することを考えます。 よくこの手の問題で解説されているのは です。 確かに、次数的には \(y\) についての \(2\) 次方程式となるため、処理しやすいという点ではメリットがあります。 ただし、注意していなかったり、根本的な理解に努めていないと事故る可能性も秘めています。 (【総括】でも少し触れています) それに対して、 も考えられます。 そうなると、\(x^{2}+(ax^{2}+b)^{2}=1\) となり、整理すると \(a^{2}x^{4}+(2ab+1)x^{2}+b^{2}-1=0\) という \(x\) に関しての 4 次方程式が登場します。 とは言え、見かけ上は4次ですが、\(x^{2}\) を塊と見れば実質は2次の処理でいけます。(複2次の形) 確かに というように、共有点の個数が4個あるようなケースもあるため、 実数解の個数と共有点の個数がリンクして考えやすい というメリットがあります。 用意した解答は の2路線用意してあります。 このケースは \(-1 \lt b \lt1\) であれば、\(a\) の値に関わらず成立します。 直感的に明らかですが、式的にバックボーンを立てようと思うと、\(y\) を消去する【路線2】の方がやりやすいと思います。 (このあたりは【解答】で確認してください。) のケースは【路線1】で得る \(y\) の2次方程式が重解をもつという翻訳で進めるのが基本路線ですが、ただ重解をもつだけでなく、\(-1 \lt y \lt 1\) の範囲内に重解をもつという部分まで考える必要があります。 なお、 \(y\) の2次方程式が重解をもつということは、判別式が \(0\) ということになります。 なぜ、判別式が \(0\) という処理をした際、 という状況が出てきて や は出てこないのか これについては【総括】の後で触れています。 ヒントは「重解」という言葉の意味を分かっていますか?ということです。 というケースなので、直感的に \(b=-1\) のときというのは分かると思います。 ただ、それはあくまで必要条件で、それで十分かと言われるとマズいですね。 ということも考えられるわけです。 つまり、開き具合を司る \(a\) はある程度大きくないといけないわけです。 このあたりをどのように式に教えてもらうかについても【路線1】【路線2】双方でマスターしましょう。 ※このあたりは曲率半径の話題とも関わってきますが、その話は別の機会にします。 むしろ、これが一番分かりやすいかもしれません。 【路線1】の \(y\) の2次方程式の解の意味(交点の \(y\) 座標という意味)も見えやすいです。 【路線2】の \(x\) の4次方程式の解の意味(交点の \(x\) 座標という意味)も見えやすいです。 個人的にこれが (1) でもいいんじゃないかとさえ思います。 (2) が今回の話題の円と放物線の共有点の個数に関する考察です。 例題と違い、今回の円 \(C\) には対称性がありません。 したがって、文字消去する際の判断力も問われます。 また、円 \(C\) を のどちらで設定するかという判断力も問われます。 この選択によって微妙にとる態度が変わってくると思います。 解答を聞くだけではもったいない問題で、このあたりを考えるのも一興です。共有点を考察するにあたって
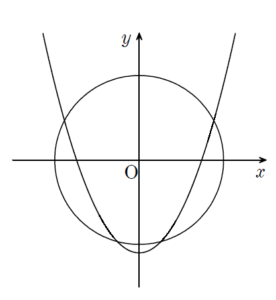
共有点が2個のケース【(1) について】
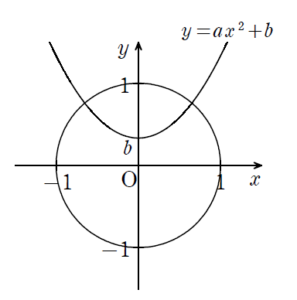
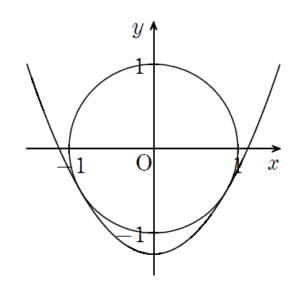
そこで問題提起

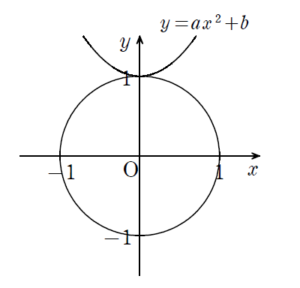
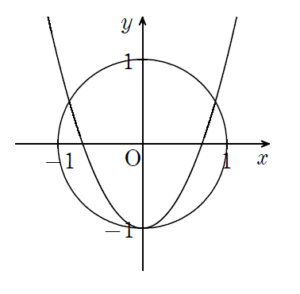
共有点が3個のケース【(2) について】

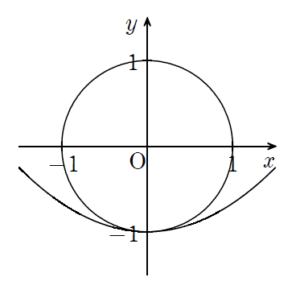
共有点が4個のケース【(3) について】

類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)


