問題はこちら(画像をクリックするとPDFファイルで開きます。)
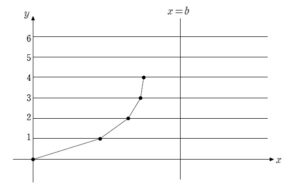
座標平面上において折れ線状に動く点の動きを考察する問題です。
「点 \(P\) が \(x=b\) を横切る」ということを式的に論じるにはどうすればよいか
について翻訳力が問われるでしょう。
(以下ネタバレ注意)
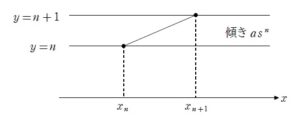
+ クリック(タップ)して続きを読む イメージの把握 のように \(y\) の値が整数になるごとに傾きが \(s\) 倍になっていきます。 イメージとしては媒質の異なる層を光が屈折していくような感じでしょうか。 確かに条件次第で \(x=b\) に達しないこともありそうです。 設定 式的にまずは点 \(P\) の \(x\) 座標について考える必要があります。 点 \(P\) の \(y\) 座標が整数に達するごとに傾きが変化していくので、\(P\) の \(y\) 座標が \(n\) となるとき \((x_{n} \ , \ n)\) と設定します。 \(x=b\) を横切るかどうかについて考えるわけですから、このように \(x\) 座標を設定して考えるわけです。 最終的なオチの想定 「\(x=b\) を横切らない」ということが分かりやすそうです。 どんなに頑張っても \(P\) の \(x\) 座標が \(b\) に達することがない、つまり \(\displaystyle \lim_{n \to \infty} x_{n} \leq b\) と表現できます。 逆に、 \(x=b\) を横切るということは \(\displaystyle \lim_{n \to \infty} x_{n} \gt b\) ということです。 等号の有無には気をつけましょう。 \(\displaystyle \lim_{n \to \infty} x_{n}=b\) ということは \(x_{n}\) は限りなく \(b\) に近づくということであり、 \(b\) そのものにはならないことに注意してください。 \(x_{n}\) を出すために 水平方向の幅に注目し、\(x_{n+1}-x_{n}\) という階差数列に注目します。 という状態であり、傾きに注目すれば、\(\displaystyle \frac {1}{x_{n+1}-x_{n}}=as^{n}\) ということになるため、 \(x_{n+1}-x_{n}=\displaystyle \frac{1}{as^{n}}\) と階差数列を得ることになります。 ここからは先ほどの目論見通り、一般項 \(x_{n}\) を出し、極限に関する考察になります。 総合的に など合格者にとっての基礎力を要する良問です。