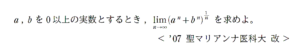今回考えてもらう問題はコチラです。
類題２はこちら（画像をクリックするとPDFファイルで開きます。）
「類題２？」と思うかもしれませんね。
この京都大学の問題はただの極限計算と言いつつも、意外と出来が芳しくないタイプの問題です。
この問題が難なくクリアーできる受験生は問題ありませんが、右往左往するようであれば、目線が定まっていません。
この目線をしっかりと固定するための例題と類題１を準備します。
類題２で右往左往するようであれば、例題、類題１をマスターしてからもう一度チャレンジしてみてください。
恐らく見える景色が変わります。
ここからスライドボックスで隠します。
+ クリック（タップ）して続きを読む \(\displaystyle \lim_{n \to \infty}(2^{n}+3^{n})^{\frac{1}{n}}\) であれば $$\begin{eqnarray} というように、 基本
より強きもので括る という態度がモノを言います。 これについては極限計算における常套手段の一つです。 今回の一般論 \(\displaystyle \lim_{n \to \infty}(a^{n}+b^{n})^{\frac{1}{n}}\) であれば ということに注目したくなるでしょう。 そうなると という場合分けを自然に行いたくなるはずです。 要領自体は上で行った具体例とほぼ同じです。 この問題も一般化してしまい \(\displaystyle \lim_{n \to \infty}\displaystyle \frac{1}{n} \log{(a^{n}+b^{n})}\) を求めてしまいます。 この一般論において \(b=a^{2}\) とすればいいわけです。 そして、この一般論は \(\displaystyle \lim_{n \to \infty} \log{(a^{n}+b^{n})^{\frac{1}{n}}}\) であり、本質的には例題と同じです。例題はこちら（画像をクリックするとPDFファイルで開きます。）
類題１はこちら（画像をクリックするとPDFファイルで開きます。）
例題について
例題はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
例えば
\displaystyle \lim_{n \to \infty}(2^{n}+3^{n})^{\frac{1}{n}}&=&\displaystyle \lim_{n \to \infty}\{3^{n}\{(\displaystyle \frac{2}{3})^{n}+1\}\}^{\frac{1}{n}} \\
&=&\displaystyle \lim_{n \to \infty}3 \cdot \{(\displaystyle \frac{2}{3})^{n}+1\}^{\frac{1}{n}}\\
&=&3
\end{eqnarray}$$一般論では
類題１について
類題１はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
類題２について
類題２はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
例題を経由していると目線が定まっているでしょう。