定点からの見込む角が等しくなる点の軌跡【2008年度 東京大学】

座標平面上での角度の扱い

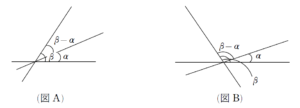
平面座標において角度を扱おうと思うと

という路線が考えられます。

今回はベクトルの内積を用いる方針、傾きと \(\mathrm{tan}\) の関係を用いる方針の２路線を検討します。

傾きと \(\mathrm{tan}\) の関係を用いる方針

通常、傾きと \(\mathrm{tan}\) の関係を用いる場合、

• 角度に向きを与え、反時計回りを正の向きとして測る

というのが得策で、これによりなす角を統一的に扱うことができます。

例えば

というように、水平ラインから反時計回りに測るわけです。

これにより、なす角 \(\beta-\alpha\) について

\(\tan{(\beta-\alpha)}=\displaystyle \frac{\tan{\beta}-\tan{\alpha}}{1+\tan{\beta} \tan{\alpha}}\)

として計算できるわけです。

しかし、この計算結果、\(\tan{(\beta-\alpha)}\) の値が負として出てきた場合、（図Ｂ）のように \(\beta-\alpha\) が鈍角ということになります。

通常、なす角と言えば、小さい鋭角の方を指しますから、この場合 \(\pi\) から引いたものをなす角と見なすわけです。

今回の \(\angle{\mathrm{APC}}\) ,  \(\angle{\mathrm{BPC}}\) は図形的な角度であり、符号付きの角度ではないため、この路線は色々ウルサイことになりそうです。

ベクトルの内積を用いる方針

\(0\) から \(\pi\) までの範囲の各 \(\alpha\) ,  \(\beta\) について

\(\alpha=\beta \  \ \Leftrightarrow \  \ \cos{\alpha}=\cos{\beta}\)

であり、角度と \(\mathrm{cos}\) の値が１対１対応します。

ベクトルの内積を用いる方針は、計算が重たくなる傾向にありますが、今回はベクトルの内積を用いて \(\mathrm{cos}\) 経由で処理した方が得策です。

\(\mathrm{P}\) \((X \ , \ Y)\) とおき、

\(\cos{\angle{\mathrm{APC}}}=\cos{\angle{\mathrm{BPC}}}\)

すなわち

$$\displaystyle \frac {\overrightarrow{\mathrm{PA}} \cdot \overrightarrow{\mathrm{PC}}}{|\overrightarrow{\mathrm{PA}}||\overrightarrow{\mathrm{PC}}|}=\displaystyle \frac {\overrightarrow{\mathrm{PB}} \cdot \overrightarrow{\mathrm{PC}}}{|\overrightarrow{\mathrm{PB}}||\overrightarrow{\mathrm{PC}}|}$$

を計算・整理していくと

\(\sqrt{X^{2}+Y^{2}+1+2X}(X^{2}-X+Y^{2}+Y)=\sqrt{X^{2}+Y^{2}+1-2X}(X^{2}+X+Y^{2}+Y)\)

という部分までは整理できると思います。

ベクトルで処理しようとした人の多くはここで手が止まってしまう可能性が大きいでしょう。

この後の処理

ここから手を進めるためには当然、ルートを捌くために、両辺２乗することを考えます。

ただ、勝手に２乗すると

同値性が崩れる

ということになってしまいます。

同値性が保たれるためには

• \(X^{2}-X+Y^{2}+Y\) と \(X^{2}+X+Y^{2}+Y\) が同符号

ということが必要となってきます。

この下で両辺を２乗すると

\((X^{2}+Y^{2}+1+2X)(X^{2}-X+Y^{2}+Y)^{2}=(X^{2}+Y^{2}+1-2X)(X^{2}+X+Y^{2}+Y)^{2}\)

ということになります。

「これを展開するの？」

と泡を吹きそうになりますが、現実的にこれを捌ききるために一工夫します。

多分、聞けば「そんなことか」と思うでしょうが、実際試験場で冷静に処理できるかというと難しいと思います。

ここから先は考えた上で、【解答】をご確認ください。

解答はコチラ