問題はこちら(画像をクリックするとPDFファイルで開きます。)

外心に関する論証問題です。
本問は名古屋大学の問題ですが、雰囲気は京大に近い感じですね。
昔の名古屋大学って結構切れ味が鋭い論証を要求していた時代もあって、個人的に割と好みだったりします。
最近の名古屋大学の問題はスタミナが必要な問題が多くて、昔と比べると問題の雰囲気も変わってきているなと感じます。
本問は誘導がないので、方針を自分で立てる必要があります。
普段の学習においては場当たり的に解くことなく、こういった方向性で進めようという構想をもって解き進めていくことが大切だと思います。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
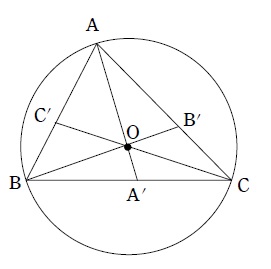
絵を描いてみると

という状況であり、
\(\overrightarrow{ OA' }=a\overrightarrow{ OA }\) , \(\overrightarrow{ OB' }=b\overrightarrow{ OA }\) , \(\overrightarrow{ OC' }=c\overrightarrow{ OC }\) と表すことができると思います。
もちろん、この \(a\) , \(b\) , \(c\) というのは \(\alpha\) , \(\beta\) , \(\gamma\) で表せるのでしょう。
そして、\(|\overrightarrow{ OA' }|=|\overrightarrow{ OB' }|=|\overrightarrow{ OC' }|\) と繋いでいくことで \(\alpha\) , \(\beta\) , \(\gamma\) に関する等式が得られるのでしょう。
それを目指す方向として見据えながら計算していくことになります。
\(A'\) , \(B'\) , \(C'\) というのは闇雲な点ではなく、条件をもった点です。
例えば \(A'\) というのは
直線 \(OA\) 上 かつ 直線 \(BC\) 上
ということが言えます。
直線上の点の位置ベクトル
位置ベクトルの基準を \(O\) とする。
直線 \(AB\) 上の点 \(P\) は \(s+t=1\) を満たす実数 \(s\) , \(t\) を用いて
\(\overrightarrow{ OP }=s \overrightarrow{ OA }+t \overrightarrow{ OB }\)
と表すことができる。
証明
直線 \(AB\) 上の点 \(P\) は
\(\overrightarrow{ OP }=\overrightarrow{ OA }+t \overrightarrow{ AB }\)
\(=\overrightarrow{ OA }+t (\overrightarrow{ OB }-\overrightarrow{ OA })\)
\(=(1-t) \overrightarrow{ OA }+t \overrightarrow{ OB }\)
\(1-t=s\) とおけば、
\(\overrightarrow{ OP }=s \overrightarrow{ OA }+t \overrightarrow{ OB }\) ( ただし , \(s+t=1\) )
と表せる。
というように「この点は直線◎◎にある」ということを「ベクトル語」で自在に翻訳できるようにしておきましょう。
ちなみに本問の結果は
\(\triangle ABC\) と \(\triangle A'B'C'\) の外心が一致するならば , \(\triangle ABC\) は正三角形
ということを意味します。
解答はコチラ