問題はこちら(画像をクリックするとPDFファイルで開きます。)
回転放物面を扱った問題で、昔より出題は控えめになりましたが、一度は扱っておきたい話題です。
3頂点 \(A , B , C\) が曲面 \(S\) 上にあるという条件は
曲面 \(S\) の方程式を出して、パラメータ表示する
と翻訳するのが最もストレートな方針でしょう。
この回転曲面 \(S\) の方程式を出す方法を本問を例にとって手順化すると以下のようになります。
step
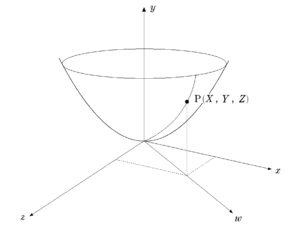
1\(S\) 上の任意の点\( (X , Y , Z)\) を持ち出し、正射影する。
ここでは \((X , 0 , Z)\) と \(zx\) 平面に正射影したとします。
step
2原点から正射影した点に伸ばした半直線を \(w\) 軸などとおき , \(wy\) 平面を考える。
\(w\) 座標は \(\sqrt{X^2+Z^2}\) となります。
step
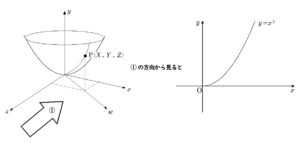
3\(w\) , \(y\) の関係は、回転前の \(x\) , \(y\) の関係と同じ
\(x\) だの \(y\) だの \(w\) だの考えるとごちゃごちゃする人もいるかもしれません。
要するに \((縦)=(横)^2\) という関係は保ったままです。
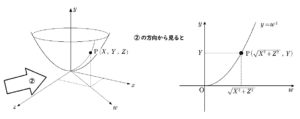
これにより、\(Y^2=X^2+Z^2\) を得ます。
\(S\) 上の任意の点 \((X , Y , Z)\) に対して \(Y^2=X^2+Z^2\) が成り立つということは、曲面 \(S\) の方程式が \(y^2=x^2+z^2\) であることに他なりません。
このことから
\(A (a_1 , \ a_1^2+a_2^2 , \ a_2)\)
\(B (b_1 , \ b_1^2+b_2^2 , \ b_2)\)
\(C (c_1 , \ c_1^2+c_2^2 , \ c_2)\)
とおくことで、点 \(A , B , C\) が \(S\) 上にあるということを翻訳できました。
これにより、\(OA^2 , \ OB^2 , \ OC^2 \) が立式できますから、あとは、\(AB^2\) を求めて「正四面体」という条件と結びつけます。
ただし、実際に処理してみるとなかなか手際よくいかず
という人も多いかもしれません。
(2) はまずは切り口が \(O\) を含む三角形であることを見抜きたいところです。
この三角形を \(\triangle OPQ\) と呼びます。
\(\overrightarrow{ AP }=u \overrightarrow{ AB }\) , \(\overrightarrow{ AQ }=v \overrightarrow{ AC }\)
などとおいて計算を進めると、\(\triangle OPQ\) の面積は \(PQ\) の長さに等しくなることが分かります。
\(\triangle ABC \) の重心 \(G\) に対して、\(P , \ G , \ Q\) が同一直線上にあるということさえ見抜けば
\(\displaystyle \frac{1}{u}+\displaystyle \frac{1}{v}=3\) が得られるはずです。
最後は2次関数の問題に帰着します。
回転曲面の中で最もシンプルなものは「円錐」でしょう。
円錐面の方程式も上述の手順で Get できますので、ぜひ練習してみましょう。
「円錐面の方程式が欲しいな」と思う場面も難関大ではしばしばあります。
こちらもCHECK
-

-
空間座標における回転体の体積【円錐の回転体の体積とその工夫】【2017年度 東京大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) (1) は難関大志望者であれば、特に手が止まることはないでしょう。 点 \(P\) の軌跡が円となることも容易に把握できる ...
続きを見る


