問題はこちら（画像をクリックするとPDFファイルで開きます。）
円に沿って動く接線の通過領域について考えるという問題です。
\(t\) の値によらず円に接しているという、強力な事実が先に与えられているため、(2) の通過領域については (1) が求まればなんとかなりそうです。
範囲付きの処理となるため、そのあたりがどこまで処理量に響いてくるかが問題かなというのが第一印象でしょう。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む 様々な解法が考えられます。 ひとまず円の中心を \((a \ , \ b)\) , 半径を \(r\) とします。 \((1-t^{2})x-2ty-t^{2}-1=0\) と、円 \(C\) が接するための条件は、中心とこの直線との距離が半径 \(r\) に等しいということであり、 \(\displaystyle \frac{|(1-t^{2})a-2tb-t^{2}-1|}{\sqrt{(1-t^{2})^{2}+4t^{2}}}=r\) ということになります。 ざっくり言えば、「この等式が \(t\) の値に関わらず成立する」ということですから、 として処理していきたくなると思います。 絶対値の処理については無理に２乗せず、場合分けによって絶対値を外す方が得策でしょう。 「\(t\) としての値に関わらず」 という条件を 「任意の \(t\) に対して」 と、全称命題として捉えることも有力です。 任意の \(t\) に対して \((1-t^{2})x-2ty-t^{2}-1=0\) という直線が円 \(C\) に接するのだから という屁理屈をかますわけです。 屁理屈をどんどん言っていくと ということになり、 という状況から \(x^{2}+y^{2}=1\) という円が浮き彫りになってきます。 ただ、もちろんこれが任意の \(t\) に対して接するかどうかという保証はありませんから、その保証をして初めて答えとしての資格を得ます。 このように全称命題の倒し方は 「任意の〇〇に対して ～～ が言える」 → 「じゃあ」特別この〇でも～～が言えるってことだよな？ という屁理屈をかまして、答えの候補を浮き彫りにさせるという態度です。 これについては、ある程度の経験が必要な上級テーマであり、場数を踏みたい方は テーマ別演習：全称命題 も参考にしてください。 直線の通過領域について、目で追っていくことが中々難しい場合は 逆像法 による解法が有力です。 ただ、今回の場合は、円に沿って動く接線を考えるということで、ある程度目で追っていくことが可能でしょう。 目で追っていける場合は目で追っていった方が早いに決まっています。 なので、今回は逆像法の解答については見送り、目で追っていくことに集中する方針を考えることにします。 目で追いきることが難しい問題については テーマ別演習：逆像法 でも扱っており、通過領域に関しては第３講で扱っています。 (1) で正しく接点が得られていれば \((\displaystyle \frac{1-t^{2}}{1+t^{2}} \ , \ -\displaystyle \frac{2t}{1+t^{2}})\) と得られています。 \(t \geq1\) という \(t\) に範囲が付く以上、接点も \(x^{2}+y^{2}=1\) 上をまるごと動くということにはならないでしょう。 よって、この接点が動き得る範囲について考えるのが自然な流れです。 \(x\) 座標の \(\displaystyle \frac{1-t^{2}}{1+t^{2}}\) については 定跡
頭でっかちは嫌われる というセオリーにしたがい、帯分数に直せば範囲が見えてきます。 \(y\) 座標の\(-\displaystyle \frac{2t}{1+t^{2}}\) については逆数をとると 相加平均・相乗平均の関係 をインスピレーションさせる形が登場します。 相当学習している受験生は ワイエルシュトラスの置換 \(\tan{\displaystyle \frac{\theta}{2}}=t\) とおいたとき、 \(\sin{\theta}=\displaystyle \frac{2t}{1+t^{2}}\) \(\cos{\theta}=\displaystyle \frac{1-t^{2}}{1+t^{2}}\) \(\tan{\theta}=\displaystyle \frac{2t}{1-t^{2}}\) と表せる。 ということを想起するかもしれません。 今回与えられた直線 \((1-t^{2})x-2ty=1+t^{2}\) は \(\displaystyle \frac{1-t^{2}}{1+t^{2}} x-\displaystyle \frac{2t}{1+t^{2}} y=1\) と変形できます。 \(y\) の係数の符号がマイナスであることに注意しつつ、ワイエルシュトラスの置換により \(t=\tan{(-\theta)}\) とおくと \((\cos{2\theta})x+(\sin{2\theta})y=1\) となり、円 \(x^{2}+y^{2}=1\) 上の点 \((\cos{2\theta} \ , \ \sin{2\theta})\) における接線であることを意味します。 (2) の \(t \geq 1\) という範囲も \(-\tan{\theta} \geq 1\) ということで、\(\theta\) の範囲が分かりますから、接点 \((\cos{2\theta} \ , \ \sin{2\theta})\) の動き得る範囲も分かります。 ワイエルシュトラスの置換については 今回は「ワイエルシュトラスの置換」と呼ばれる有名な置換を用いた問題を扱います。 ワイエルシュトラスの置換とは ワイエルシュトラスの置換とは ワイエルシュトラスの置換 \(\ ... 続きを見る でスポットを当てています。(1) について
路線１：恒等式としての処理
路線２：全称命題としての処理
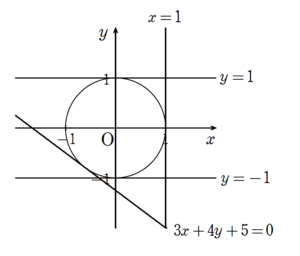
(2) について
ウンチク
参考ワイエルシュトラスの置換【三角関数のうまい置き換え】【2004年度 山口大学ほか】