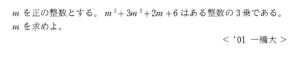例題はこちら(画像をクリックするとPDFファイルで開きます。)

類題はこちら(画像をクリックするとPDFファイルで開きます。)

例題の最終的なオチは与えられた2次式が平方数になるような \(n\) を求めるという問題です。
ノーヒントだと適度に差が付くレベルの問題になるでしょう。
例題は誘導があるため、本気で北大を目指している受験生であれば確保して然るべきレベルとなります。
一通り解いた後、ノーヒントで出題された場合の構想についても触れてみます。
類題は与えられた3次式が立方数になる \(m\) を求めさせる問題です。
こちらはノーヒントでの出題であるため、構想まで含めて考える必要があります。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
例題について
例題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

(1) について
与えられた関係式を整理すると
\(a=(2k-1)n+k^{2}\)
となり、\(a\) が消去できます。
これにより
\(a-(k^{2}+2k-1)=\cdots=(2k-1)(n-1)\)
と差を取って \(a\) を消去した式が因数分解できます。
\(k\) , \(n\) は自然数ですからもちろんこの式は \(0\) 以上の値となります。
(2) について
\(n(n+1)+14\) は展開すると
\(n^{2}+n+14\)
で、\(n^{2}\) より大きいです。
つまり、\(n^{2}\) より大きい平方数ということになりますから
\((n+k)^{2}\)
という形で \(n\) との誤差を埋める \(k\) というパラメーターで表現できるわけです。
これにより
という等式を得ます。
これにより、(1) で \(a=14\) のときを考えることに帰着します。
つまり、
\(14 \geq k^{2}+2k-1\)
ということになり、\(k\) の範囲が絞られます。
\(k\) の範囲さえ絞られればこっちのもので、あとは個別にしらみつぶせばおしまいです。
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)

例題の3次式バージョンです。
こちらは誘導がありません。
例題の考え方が自分のものになっているかの確認としてはうってつけです。
この問題が、今後まんま出題されることを期待するような勉強ではなく、あくまで着眼点や、そこからの頭の動かし方を身につけるということを目的としてください。
例題の解答はコチラ
類題の解答はコチラ