例題はこちら(画像をクリックするとPDFファイルで開きます。)
三角関数に関する対称式の問題です。
方針自体は
(1) で立式し、(2) でその立式した式の最大最小を考える
というシンプルな流れです。
ある程度の力をもった受験生であれば、腕力でねじ伏せること自体はそこまで難しくはないでしょう。
ただ、糧となる工夫についてはぜひとも身につけたい工夫です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 与えられた状況を図示すると というような図がかけるでしょう。 \(\mathrm{OP}=1\) という条件はいわば 取っ手をもって動かす というイメージでしょうか。 幸い、点 \(\mathrm{A}\) , \(\mathrm{B}\) は各軸の正の範囲を動くので、\(\theta\) は鋭角の範囲で事足ります。 \(\mathrm{OA}\) , \(\mathrm{OB}\) , \(\mathrm{AB}\) についてどのように立式していくかについては、直角三角形による三角比の定義によって立式していけばよいでしょう。 ただ、直角三角形が沢山あり、目移りしそうです。 \(\mathrm{OA}\) がほしければ \(\mathrm{OA}\) を含む直角三角形 \(\mathrm{OAP}\) \(\mathrm{OB}\) がほしければ \(\mathrm{OB}\) を含む直角三角形 \(\mathrm{OBP}\) \(\mathrm{AB}\) がほしければ \(\mathrm{AB}\) を含む直角三角形 \(\mathrm{OAB}\) というように、欲しいものに合わせて注目する直角三角形をとらえていくという目的意識をもった立式を心がけたいところです。 (1) で正しく立式できていれば \(\mathrm{OA}+\mathrm{OB}-\mathrm{AB}=\displaystyle \frac{\sin{\theta}+\cos{\theta}-1}{\sin{\theta}\cos{\theta}}\) という式が得られます。 こいつの最小値を考えるわけですが、理系の方であればここから 微分でねじ伏せる という力業でもいけなくはないでしょう。 試験場で何も浮かばなければそのような方針もやむなしです。 ただ、学習段階においては今回の式の形の特徴を見落とさず、相応の工夫をすることで倒したいところです。 今回立式した式の形 \(\displaystyle \frac{\sin{\theta}+\cos{\theta}-1}{\sin{\theta}\cos{\theta}}\) を観察し、 \(\sin{\theta}\) , \(\cos{\theta}\) を入れ替えても元の式と不変 ということに気が付いたらしめたものです。 いってみたら、 \(\sin{\theta}\) , \(\cos{\theta}\) についての対称式 ということです。 そこで、 急所
\(t=\sin{\theta}+\cos{\theta}\) と、和を \(t\) という文字でおいてやります。 両辺2乗することで、 \(t^{2}=\sin^{2}{\theta}+\cos^{2}{\theta}+2\sin{\theta}\cos{\theta}\) すなわち \(\sin{\theta}\cos{\theta}=\displaystyle \frac{t^{2}-1}{2}\) と、積も Get できます。 対称式は基本対称式である和と積であらわせるわけですから、\(\sin{\theta}\) , \(\cos{\theta}\) についての対称式については \(t=\sin{\theta}+\cos{\theta}\) とおくことで、\(t\) の関数に置き換えることができるわけです。 この 2乗することで積が Get できる という部分に「言われりゃそうだけど」という天下り感を感じた人のために、それを少しでもぬぐう解説を【総括】の中でしてあります。 原題には置き換えの指示がありましたが、例題でパワーアップした皆様にとってみれば余計なお世話以外の何物でもないと思いますのでカットさせてもらいました。 例題で得た力を存分に発揮してみてください。状況を図示すると
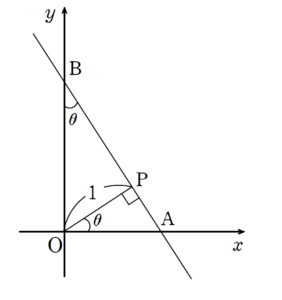
(2) について
三角関数の対称式
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)


