問題はこちら(画像をクリックするとPDFファイルで開きます。)
三角形の長さに関する整数問題です。
図形ならではの隠れた条件などに目を光らせないと、手が止まってしまったり、手際が悪くなってしまったりします。
京大の「らしさ」が感じられる良問です。
スムーズに式変形ができれば、問題ないですが、手が止まってしまったときのリカバリーについても触れてあります。
結論から言えば、セオリーに基づいて式変形すればできなくはないので、諦めずに粘り勝ちを狙っていくことも可能です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む ひとまずは状況を図示してみると という状況です。 この状況を立式しようと思うと、第一感は余弦定理です。 これにより $$\begin{eqnarray} という関係式を得ます。 ここから、 \(b^{2}=(a-c)^{2}+ac\) として、 \(b^{2}-(a-c)^{2}=ac\) と、\(〇^{2}-□^{2}\) の形からの因数分解を狙っていくことが考えられます。 整数問題において、因数分解という積の形を狙っていくことは常套手段の一つです。 これにより、 \((b+a-c)(b-a+c)=ac\) という形に因数分解できます。 \(a\) , \(c\) が素数であることも効いてきて、整数問題の常套手段の一つ ポイント
積の形からの約数拾い を考えることができます。 整数問題の有力方針 についてはしっかりと学習しておきましょう。 闇雲に力ずくで押し通しても無駄に労力とエネルギーを使うため、省エネ出来る部分は省エネしましょう。 今回、\(a\) , \(c\) は対等な立場であり、\(a \geq c\) という大小関係で考えても一般性を失いません。 そうなってくると \(b+a-c \geq b+c-a \gt 0\) ということになりますから $$\begin{eqnarray} または $$\begin{eqnarray} という2パターンを考えれば事足りることになります。 この後の詰めについては解答 PDF をご覧ください。 \(b^{2}=(a-c)^{2}+ac\) として、 \(b^{2}-(a-c)^{2}=ac\) を狙っていく路線1は \(〇^{2}-□^{2}\) の因数分解を狙っていくことを考えたとしても、スムーズに出てくるかどうかは別問題でしょう。 そこで、もっと基本に立ち返って ポイント
文字の整理は1文字中心 というセオリーに従って変形してみます。 ここでは \(a\) について整理して \(b^{2}=a^{2}-ca+c^{2}\) という \(a\) についての 2 次式と見ます。 ここから、 \(b^{2}=(a-\displaystyle \frac{c}{2})^{2}+\displaystyle \frac{3c^{2}}{4}\) と平方完成します。 というのも、人間は2カ所で変数が動かれると鬱陶しく感じるものです。 2カ所で動く変数を一カ所に集めることは数学において有効な方向性なのです。 平方完成は、変数を一カ所に集めるための有効な手段の一つです。 さて、分母を払えば \(4b^{2}=(2a-c)^{2}+3c^{2}\) ということで \(4b^{2}-(2a-c)^{2}=3c^{2}\) \((2b+2a-c)(2b-2a+c)=3c^{2}\) と、無事因数分解が完了し、右辺も \(c\) が素数であることから約数を拾っていけそうです。 この後の詰めについては、若干煩わしいですが、 これは知らなきゃ無理でしょ~ 的な無茶な話は出てこない(はず)で、最低限の観察力さえあれば手なりに進んでいくはずです。長さや角度に関する条件の立式
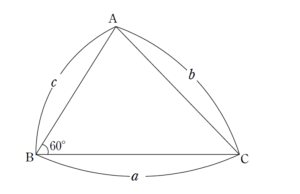
b^{2} &=& a^{2}+c^{2}-2ac\cos{60^{\circ}} \\
&=& a^{2}+c^{2}-ac
\end{eqnarray}$$路線1:積の形を狙った因数分解
労力を減らす
\left\{
\begin{array}{l}
b+a-c = a \\
b+c-a = c
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
b+a-c = ac \\
b+c-a = 1
\end{array}
\right.
\end{eqnarray}$$路線2:文字の整理は1文字中心

