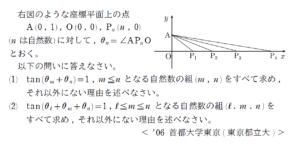
例題はこちら(画像をクリックするとPDFファイルで開きます。)
マチンの公式とその周辺の等式について触れることができる問題を紹介します。
表向きは \(\tan{ \ }\) が絡む整数問題という顔をしています。
背景的なものを抜きにした整数問題として見てもいい訓練となる問題であり、整数問題の実戦的な問題として丁度よいレベルの良問でしょう。
(以下ネタバレ注意)
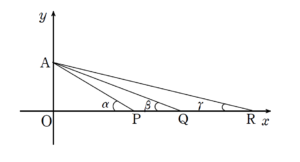
+ クリック(タップ)して続きを読む というように、ひとまず角度 \(\alpha\) , \(\beta\) , \(\gamma\) と見やすく名前をつけておきます。 このとき という関係式が成り立ちます。 (1) は \(p\) の範囲が限られることを示唆する設問です。 \(p\) の範囲が限られるということはそれに関連する角度 \(\alpha\) についても範囲が限られることになるでしょう。 \(\alpha+\beta+\gamma=\displaystyle \frac{\pi}{4}\) という条件から、これら一つ一つの角度は \(\displaystyle \frac{\pi}{4}\) 未満です。 ゆえに、\(\alpha \lt \displaystyle \frac{\pi}{4}\) であることはある意味すぐに見えます。 一方で、角度を均等に分け合うとしたら \(\displaystyle \frac{\pi}{12}+\displaystyle \frac{\pi}{12}+\displaystyle \frac{\pi}{12}=\displaystyle \frac{\pi}{4}\) です。 そうなってくると一番大きな角度である \(\alpha\) は小さくても \(\displaystyle \frac{\pi}{12}\) であることが見えるでしょう。 これより \(\displaystyle \frac{\pi}{12} \leq \alpha \lt \displaystyle \frac{\pi}{4}\) という形で、\(\alpha\) の範囲が絞られます。 今はラフに考えましたが、【解答】ではもう少しフォーマルに記述していきたいと思います。 \(\beta+\gamma=\displaystyle \frac{\pi}{4}-\alpha\) と見て、両辺に \(\tan{ \ }\) の服を着せてやると \(\tan{(\beta+\gamma)}=\tan{(\displaystyle \frac{\pi}{4}-\alpha)}\) ということになります。 加法定理によって \(\displaystyle \frac{\tan{\beta}+\tan{\gamma}}{1-\tan{\beta}\tan{\gamma}}=\displaystyle \frac{\tan{\displaystyle \frac{\pi}{4}}-\tan{\alpha}}{1+\tan{\displaystyle \frac{\pi}{4}}\tan{\alpha}}\) となり、先ほどの を代入して整理すると \(\displaystyle \frac{q+r}{qr-1}=\displaystyle \frac{p-1}{p+1}\) という関係式を得ます。 (1) によって \(p\) の値は限られていますから、あとは各々の \(p\) の値に対して個別検証ということになります。 その際、整数問題としては典型的な形である不定方程式が現れます。 ここから先は打ち損じることは許されません。 本問を正しく解ききると得られる \((p \ , \ q \ , \ r)=(2 \ , \ 4 \ , \ 13) \ , \ (2 \ , \ 5 \ , \ 8) \ , \ (3 \ , \ 3 \ , \ 7)\) が意味することは、\(y=\tan{x}\) の逆関数 \(\arctan{x}\) に対し ということを意味します。 このことに関連する話題として「マチンの公式」と呼ばれる次のような等式があります。 マチンの公式 \(4\arctan{\displaystyle \frac{1}{5}}-\arctan{\displaystyle \frac{1}{239}}=\displaystyle \frac{\pi}{4}\) 本問を通じて分かるように、このマチンの公式にはそれに準ずるような類似形が多々あります。 例えば有名なものとしてはオイラーの発見したとされる \(\arctan{\displaystyle \frac{1}{2}}+\arctan{\displaystyle \frac{1}{3}}=\displaystyle \frac{\pi}{4}\) などがあります。 本問の復習をしつつ、これについて触れた問題を類題としたいと思います。 (1) が上で述べたオイラーの発見した形の導出になっています。 (2) は例題の復習ですが、条件の与えられ方が若干異なるので、記述面では少し気を付けてください。 今回の話題はフィボナッチ数列とも絡みがあり、 問題はこちら(画像をクリックするとPDFファイルで開きます。) tanとフィボナッチ数列が面白く絡んでいる問題を見てみます。 tanとはタンジェントです。炭治郎ではありません。 ただ、全集中で解いてみ ... 続きを見る も併せて考えて見ると面白いと思います。図示してみると
(2) について
今回の結果とマチンの公式
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)
追記

参考tanとフィボナッチ数列【マチンの公式との関連】【2013年度 京都府立医科大学】