問題はこちら（画像をクリックするとPDFファイルで開きます。）
問題を読んでみると、「えっ、マジ？」と言いたくなる結果です。
まぁそれもそのはずで、「ポンスレの閉形定理」というものが背景にあります。
ポンスレの閉形定理
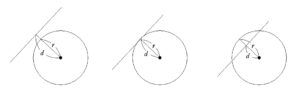
２つの２次曲線 \(C_{0}\) , \(C_{1}\) , \(3\) 以上の自然数 \(n\) について
\(C_{1}\) 上のある点を１つの頂点として \(C_{0}\) に外接し , \(C_{1}\) に内接する \(n\) 角形が１つでも存在すれば , \(C_{1}\) 上の任意の点についてそれを１つの頂点とする同様の \(n\) 角形が存在する。
この辺の時代で流行っていたらしく、1990年度に東京大学、京都大学がこれをネタにした問題を出題していました。
実際に問題を解くときには、そんな知識の有無など差にはならないので、安心してください。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む (1)についてですが、線分 \(QR\) の中点 \(M\) の座標は \((\displaystyle \frac{b+c}{2} \ , \displaystyle \frac{b^{2}+c^{2}-4}{2} )\) と対称式を含む形ですから、\(b+c\) や \(bc\) などの基本対称式が得られたらいいな、という心構えで進めていきます。 (2) はやることは明確で、直線 \(QR\) と \(S\) の中心 \((0 \ , \ 0)\) との距離が \(S\) の半径である \(1\) と等しいことを言うのが目標です。 また、円と直線が接するということの翻訳については という方法があります。 直線と円の中心の距離を \(d\) , 円の半径を \(r\) としたとき 円と直線の位置関係 ということが言えます。 円と直線の位置関係を記述するにあたっては、判別式の路線は計算量が膨らみがちです。 なので、円と直線の位置関係を扱う際には大抵、点と直線の距離を利用する方法で処理するということは知っておきましょう。 復習用の類題を用意しました。 例題で扱った名古屋大学の構図を \(y\) 軸方向に \(+2\) 平行移動した構図だということが分かると思います。 さらに、\(A\) の座標が具体的なものになっているという点で、扱いやすくなっています。 【総括】のあとに【検証】という項目を立てて、\(A\) \((a \ , \ a^{2})\) という一般論にして、本問の主張も検証してあります。
追記
問題はこちら（画像をクリックするとPDFファイルで開きます。）
