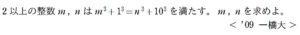問題はこちら(画像をクリックするとPDFファイルで開きます。)

問題自体は不定方程式を解くという整数問題における典型的な話題です。
ただ、この問題の背景にある逸話が面白く、「ラマヌジャンのタクシー数」という逸話をもとにした問題です。
(どちらかというと読み物的な感じです)
【総括】のあとにその逸話について載せておきましたので、ぜひご覧ください。
一応ここでも折りたたんでおくので、興味があれば+マークをクリック(タップ)して読んでみてください。
+ ラマヌジャンのタクシー数の逸話について
ラマヌジャンは
\( \displaystyle\frac{1}{\pi}=\displaystyle\frac{2\sqrt{2}}{99^{2}}\displaystyle \sum_{n=0}^\infty \displaystyle\frac{(4n)!(1103+26390n)}{4^{n}\cdot99^{n} \cdot n!} \)
\( \displaystyle\frac{4}{\pi}=\displaystyle \sum_{n=0}^\infty \displaystyle\frac{(-1)^{n}(4n)!(1123+21460n)}{882^{2n+1}\cdot(4^{n}\cdot n!)^{4}} \)
など、どこから思いついたのかと思うような等式を次々と発見した直感型の天才です。
しかし、彼には証明という概念がなく、「夢でナーマギリ女神が教えてくれた」などと直感に頼りすぎていたため、後の数学者がこれらの問題を証明するのに苦労しました。
ただ、その直観力はずば抜けて鋭く、彼がいなかったらこれらの等式は発見されなかったのではないかとさえ言われています。
彼はハーディーという数学者に才能を見出され、ケンブリッジ大学に招聘されることになるのですが、ハーディーは下手に手を加えてラマヌジャンの才能が失われるのを恐れ、必要以上に手を加えることをしませんでした。
そんな中、イギリスでの生活に馴染めず、ラマヌジャンは療養することになります。
ある日、療養中のラマヌジャンを見舞いに来たハーディーが
「乗ってきたタクシーのナンバーは \(1729\) だった。たいして特徴のない数だったよ。」
と言いました。
これを聞いたラマヌジャンはすぐさま
「そんなことはありません。\(1729\) は
\(1729=12^{3}+1^{3}=9^{3}+10^{3}\)
と2通りの立方数の和で表せる数の中で最小のものです。」
と答えたそうです。
この話は、ラマヌジャンの数に対する研ぎ澄まされ方が群を抜いている一つのエピソードとして有名であり、この \(1729\) は「タクシー数」と呼ばれています。
さて、本問を解く話題です。
いつも言っていますが、整数問題の基本手法
整数問題の有力方針
- 積の形から約数の拾い上げ
- 余りで分類
- 評価する(範囲を絞る)
を意識します。
これについては、詳しくは折りたたんでおきますので、基本をしっかりと確認したい方は以下の「+マーク」をクリック(タップ)して読んでください。
+ 基本事項を確認する
積の形から約数の拾い上げ
例題:\(x , y\) は自然数とする。\(xy+2x+3y=6\) となる \(x , y\) の値の組を全て求めよ。
解答例
与えられた方程式は \((x+3)(y+2)=12\) と変形できる。
\(x+3 , \ y+2\) はともに自然数なので
\((x+3 , \ y+2)=(1, 12) \ (2 , 6) \ (3 , 4) \ (4 , 3) \ (6 , 2) \ (12 , 1)\)
よって , \((x , \ y)=(-2 , 10) \ (-1 , 4) \ (0 , 2) \ (1 , 1) \ (3 , 0) \ (9 , -1)\)
このうち、\(x , \ y\) がともに自然数である組は
$$(x , \ y)=(1 , \ 1)$$
実際にはもう少し手際よく絞れたりしますが、このように積の形を無理やり作って \(12\) の約数を拾い上げていきます。
整数問題の中でもかなり頻出な考え方です。
余りで分類
例題:\(m\) を整数として、平方数 \(m^2\) を \(3\) で割った余りは \(2\) とならないことを示せ。
解答例
以下 , \(k\) は整数とする。
\(<1> \ \ m=3k\) のとき
\(m^2=9k^2\) で , \(m^2\) を \(3\) で割った余りは \(0\)
\(<2> \ \ m=3k\pm 1\) のとき
\(m^2=9k^2\pm6k+1=3 \ (3k^2\pm2k)+1\) で , \(m^2\) を \(3\) で割った余りは \(1\)
よって、平方数 \(m^2\) を \(3\) で割った余りは \(0\) または \(1\) に限られ、題意は示された。
今回の例題の場合、世の中の整数を \(3\) で割った余りで分類しました。
\(3k\) , \(3k+1\) , \(3k+2\) と分類してもよいのですが、\(3\) で割って \(2\) 余る数というのは
「 \(3\) の倍数から見て \(1\) 足りない数」
ということもできるため、余り \(1\) のときと、余り \(2\) のときを合わせて
\(m=3k\pm 1\) のとき
としてやるという工夫もよくやります。
また、「何で割った余りに注目するか」ということもレベルが高くなってくると大事になってきます。
評価する(範囲を絞る)
例題:\(xyz=x+y+z\) を満たす自然数 \((x , \ y , \ z)\) の組を全て求めよ。
解答例
問題の対称性からひとまず \(x \leq y \leq z\) として考える。
このとき , \(x+y+z \leq z+z+z\) であり , 条件から , \(xyz \leq 3z\)
すなわち , \(xy \leq 3\)
これより , \((x , \ y)=(1 , \ 1) , \ \ (1 , \ 2) , \ \ (1 , \ 3) \)
\(<1> (x , \ y)=(1 , \ 1)\) のとき
与えられた条件式から , \(z=2+z\) でこれを満たす \(z\) は存在しない。
\(<2> (x , \ y)=(1 , \ 2)\) のとき
与えられた条件式から , \(2z=3+z\) で , \(z=3\) を得る。
(これは \(x \leq y \leq z\) を満たす。)
\(<3> (x , \ y)=(1 , \ 3)\) のとき
与えられた条件式から , \(3z=4+z\) で , \(z=2\) を得る。
(これは \(x \leq y \leq z\) を満たさない。)
以上 \(<1>\) , \(<2>\) , \(<3>\) から
\((x , \ y , \ z)=(1 , \ 2 , \ 3)\)
実際には \(x \leq y \leq z\) という制限はないので
\((x , \ y , \ z)=(1 , \ 2 , \ 3) , \ \ (1 , \ 3 , \ 2) , \ \ (2 , \ 1 , \ 3) , \ \ (2 , \ 3 , \ 1) , \ \ (3 , \ 1 , \ 2) , \ \ (3 , \ 2 , \ 1)\)
まず今回の数たちというのはそんなに大きくないだろうことが予測されます。
普通は (積)\( \gt \)(和) にも関わらず、積と和が等しいと言っているのですから。
そして、今回の問題には「対称性」があります。
なので、いったん \(x \leq y \leq z\) という区別をつけて考えることで範囲を絞り込み、\((x , \ y , \ z)\) の組が出てきたら、その大小関係を外して答えとします。
変数が3文字以上になると、このように等式を諦めて不等式をつないでいくことが多くなると思います。
特に対称性がある整数問題ではそれを見落とさないようにしましょう。
本問についてですが、
\(m^{3}-n^{3}=(m-n)(m^{2}+mn+n^{2})\) と因数分解ができることから
\((m-n)(m^{2}+mn+n^{2})=999\)
と、積の形としてから約数を拾っていきます。
ただ、今回のように約数の数が多かったり、最終的に処理する連立方程式が面倒だったりすると、中々正面突破は厳しかったりします。
そこでどのような工夫の余地があるのかということについて考えてもらいたいのと同時に学んでほしいと思います。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
まず、実際に連立方程式に入る前に、削れる候補は削っておきます。
その際に目を向けるポイントとしては
候補削減のチェックポイント
- 符号
- 大小
- 互いに素かチェック(偶奇チェックも含め)
が主なところです。
符号についてですが、今回は(正の数)×(正の数)という形になりますので、これで労力が半減します。
大小についてですが、次数的にみて
\(m-n \lt m^{2}+mn+n^{2}\)
と分かります。(解答ではちゃんと示します。)
これでさらに労力が半減します。
互いに素かのチェックですが、本問については、\(m-n\) と \(m^{2}+mn+n^{2}\) が互いに素かどうかは言えなさそうです。
※余談ですが、偶奇チェックについては
\(A\pm B=\) (偶数) ならば \(A\) , \(B\) の偶奇が一致
\(A\pm B=\) (奇数) ならば \(A\) , \(B\) の偶奇が異なる
としてチェックすることが多いです。
これにより、
\((m-n \ , \ m^{2}+mn+n^{2})=(1 \ , \ 999) \ (3 \ , \ 333) \ (9 \ , \ 111) \ (27 \ , \ 37)\)
を得ますが、同じような2次の連立方程式を4回も解くのは腕が疲れます。
そこで
同じような手間を避ける工夫
\(\begin{eqnarray}
\left\{
\begin{array}{l}
m - n = K \\
m^{2}+mn+n^{2} = L
\end{array}
\right.
\end{eqnarray}\)
と一般的な形で文字消去して2次方程式を作っておく
という工夫をしたいと思います。
解答はコチラ