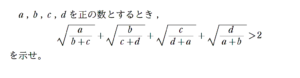問題はこちら（画像をクリックするとPDFファイルで開きます。）
難問です。
誘導があれば別ですが、今回は敢えて誘導なしで考えてみてほしいと思います。
ノーヒントで出題する大学があれば、鬼舞辻以上の鬼です。
仮に出題されたとしても、ほとんどの受験生は撃沈すると思いますので差はつかないでしょう。
「これ解かせる気ないだろ」というような出題の仕方は、あんまり自分の好みではないですが、たまにはウンウン唸る時間も必要です。
正直に言うと、自分は本問の背景にある「シャピロの巡回不等式」というものを知っていたため、純粋な目線で本問は見れなかったです。
多分その知識なしだったら撃沈していたと思います。
解けなくても自信を失う必要はないということだけは言っておきます。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む 次の有名な（マニアックな）不等式があります。 シャピロの巡回不等式 \(n\) を \(3\) 以上の整数で、かつ\(12\) 以下の偶数、または \(23\) 以下の奇数とする。 \(x_{1}\) , \(x_{2}\) , \(\cdots\) , \(x_{n}\) を正の実数とするとき、 \(\displaystyle \frac{x_{1}}{x_{2}+x_{3}}+\displaystyle \frac{x_{2}}{x_{3}+x_{4}}+\cdots+\displaystyle \frac{x_{n-2}}{x_{n-1}+x_{n}}+\displaystyle \frac{x_{n-1}}{x_{n}+x_{1}}+\displaystyle \frac{x_{n}}{x_{1}+x_{2}} \geq \displaystyle \frac{n}{2}\) が成立する。 この \(n=4\) のときである \(\displaystyle \frac{x_{1}}{x_{2}+x_{3}}+\displaystyle \frac{x_{2}}{x_{3}+x_{4}}+\displaystyle \frac{x_{3}}{x_{4}+x_{1}}+\displaystyle \frac{x_{4}}{x_{1}+x_{2}} \geq 2\) が背景的なものにあります。 この \(n=4\) の場合の証明は により、攻め落とすことができます。 なお、シャピロの巡回不等式における \(n=3\) のときである \(\displaystyle \frac{x_{1}}{x_{2}+x_{3}}+\displaystyle \frac{x_{2}}{x_{3}+x_{1}}+\displaystyle \frac{x_{3}}{x_{1}+x_{2}} \geq \displaystyle \frac{3}{2}\) という不等式は Nesbitt (ネスビット) の不等式と呼ばれています。 これについては 例題はこちら（画像をクリックするとPDFファイルで開きます。） 類題はこちら（画像をクリックするとPDFファイルで開きます。） チェビシェフの不等式と呼ばれる有名不等式を背景にもつ問題です。 例題の ... 続きを見る の記事の中で扱っています。シャピロの巡回不等式
参考チェビシェフの不等式【2017年度 立正大学ほか】
