問題はこちら(画像をクリックするとPDFファイルで開きます。)
オイラー線と呼ばれる有名な話題について扱います。
1993年度札幌医科大、2006年度岩手大、2018年度上智大など、出題校をあげていくとキリがありません。
今回は最も標準的な訊き方をしている問題を例題としてもってきました。
本問の流れやストーリー、結果は難関大を目指すにあたり記憶に値します。
(以下ネタバレ注意)
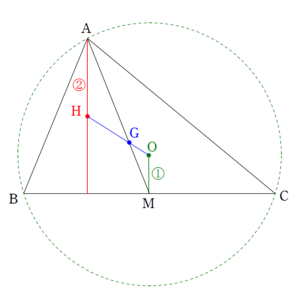
+ クリック(タップ)して続きを読む オイラー線 三角形 \(\mathrm{ABC}\) の外心を \(\mathrm{O}\) , 重心を\(\mathrm{G}\) , 垂心を \(\mathrm{H}\) としたとき \(\overrightarrow{ \mathrm{OH} }=3\overrightarrow{ \mathrm{OG} }\) が成立する。 これより , \(\mathrm{O}\) , \(\mathrm{G}\) , \(\mathrm{H}\) が同一直線上にあり、その直線をオイラー線という また、 \(\mathrm{OG} : \mathrm{GH}=1:2\) が成り立つ 本問はこの結論の証明が趣旨となっています。 重心の位置ベクトル 三角形\(\mathrm{ABC}\) の重心 \(\mathrm{G}\) に対して \(\overrightarrow{\mathrm{OG}}=\displaystyle \frac{1}{3}(\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}})\) という基本事項はもちろん常識となっている必要があります。 この \(\mathrm{O}\) は特に外心である必要はなく、一般論としての結論として与えられます。 三角形 \(\mathrm{ABC}\) の外心を \(\mathrm{O}\) としたとき、 垂心の位置ベクトル 三角形 \(\mathrm{ABC}\) の垂心 \(\mathrm{H}\) は \(\overrightarrow{\mathrm{OH}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}\) という式で与えられる。 という内容は記憶に値し、主張している内容的にもキレイな内容です。 このポイント2の証明が本問の (2) の内容です。 先ほどのポイント1の内容も考えると \(\overrightarrow{\mathrm{OH}}=3\overrightarrow{\mathrm{OG}}\) ということが言えます。 この式は、冒頭のオイラー線に関する主張を示しています。 本問はベクトル演算による代数的証明でしたが、幾何的に証明することもできます。 \(\mathrm{M}\) を辺 \(\mathrm{BC}\) の中点としたとき \(\mathrm{AH} : \mathrm{OM}=1:2\) であることが示されれば \(\triangle{\mathrm{GAH}} \sim \triangle{\mathrm{GOM}}\) より、 \(\mathrm{AG} : \mathrm{GM}=1:2\) であることがいえ、 直線 \(\mathrm{AM}\) , \(\mathrm{OH}\) の交点 \(\mathrm{G}\) が三角形 ABC の重心 \(\mathrm{G}\) ということが言えるため、証明できることになります。 問題はどのように \(\mathrm{AH} : \mathrm{OM}=1:2\) であることを示すかということです。 これについては【総括】の中で触れてあります。 また、2021年度の京大理系において、オイラー線についての見識があると即解決する問題があります。 問題はこちら(画像をクリックするとPDFファイルで開きます。) 京大にしては珍しく誘導があります。 (1) は幾何的に攻めたいですね。 2定点を見込む角度が一定ということで、円周角の定理をインスピレー ... 続きを見る よろしければご確認ください。オイラー線について
証明の骨格
ポイント1
ポイント2
幾何的な証明について

参考2021年度 京都大学理系第5問【垂心の軌跡】

