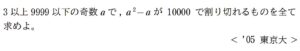問題はこちら(画像をクリックするとPDFファイルで開きます。)

約数を拾うタイプの問題で、定番の問題に見える一方、解き進めていくと、本問がもつ個性に注目して解き進める必要性も出てくるため、非常にいい問題です。様々な解法も考えられるため、教材として採用したくなりますし、実際様々な問題集などで採り上げられています。
問題自体は「積の形から約数拾い」という方針が目につく形です。
最初の一手である因数分解は恐らくすぐに気が付けると思います。
\(a(a-1)=2^{4}5^{4}M\) という形を得てから、本問ならではの個性的な部分に目を向ける必要が出てくるでしょう。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
まず、\(a\) , \(a-1\) が連続2整数なので互いに素であることに注目しないといけません。
これにより4つある2という素因数、5という素因数は素因数を分かち合うことはありません。
つまり、素因数2はどちらかにかたまり、素因数5もどちらかにかたまるということです。
\(a\) が 3 以上 9999 以下であることに注意すると
\begin{eqnarray}
\left\{
\begin{array}{l}
a= 625K \\
a-1 = 16L
\end{array}
\right.
\end{eqnarray}
と表すことができると思います。
ここからは「何が一番目につくか」です。目についた特徴によって手なりに選ぶ解法が変わってくると思います。
準備した解答例では3つほど方針を載せておりますが、それ以外にももっとあると思います。
大切なことは式のもつ特徴や個性を見落とさずに、それを活かす解法を選択し、適切に処理する力を身につけることです。
消化不良を起こさないよう、本問を通じて様々なことを学習していただきたいと思います。
解答はコチラ