問題はこちら(画像をクリックするとPDFファイルで開きます。)
\(\displaystyle \frac{1}{2}\) からスタートし、2種類の関数を用いて次々と値を出して数列を作っていくという操作について考えます。
京大らしく、シンプルな問題ですが簡単ではありません。
これまた京大の特徴の一つである「誘導がない」形式での出題なので、構想から自分で組み立てる必要があります。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 簡単な実験をしてみても、中々核心まで辿り着けないでしょう。 問題の匂いから確率漸化式を疑うことはできるかもしれませんが、2種類の関数について、どのタイミングでどちらを使うかを追っていくことが大変なので頭を抱えてしまう人も多いでしょう。 この数列がどのような振る舞いをするかを視覚的に捉えてみます。 ある関数 \(f(x)\) を用いて \(a_{n+1}=f(a_{n})\) と「代入して次、代入して次、\(\cdots\)」と定まっていく数列の振る舞いを目で見ると、次の図のようになります。 代入して得た値は、「縦軸」の値となります。 次の代入に備え、縦軸の値を「横軸」にもっていくためには \(y=x\) ( 横軸の値と縦軸の値が等しくなるようなライン ) を書き添えることで解決します。 本問の漸化式を司る関数は2種類ありますので、若干図がうるさくなりますが、本問の数列の振る舞いを視覚化すると以下のようになります。 こうしてみると、\(\displaystyle \frac{2}{3}\) という値のほかに、キーとなる数値である \(\displaystyle \frac{1}{3}\) という数字に辿り着きます。 恐らく多くの人が漸化式を立てる際 \(x_{n} \lt \displaystyle \frac{2}{3}\) となる確率を \(P_{n}\) とする。 という、本問の問題文で設定されているものを単純にそのまま運用しようとして困ってしまったのではないかと思います。 困るのは当然で、この \(\displaystyle \frac{1}{3}\) というキーナンバーに辿り着き という3種類の状態推移を考える必要があるわけです。 そこで、 と設定し、 状態 \(A_{n}\) , \(B_{n}\) , \(C_{n}\) となる確率をそれぞれ \(a_{n}\) , \(b_{n}\) , \(c_{n}\) とします。 この図から分かる通り、状態 \(A_{n}\) からは となります。 この図から分かる通り、状態 \(B_{n}\) からは となります。 この図から分かる通り、状態 \(C_{n}\) からは となります。 状態推移を捉えることができれば $$\begin{eqnarray} という連立漸化式が立式できます。 この立式ができれば、あとは漸化式の処理となります。 連立漸化式の基本は文字消去ですが、確率漸化式特有の隠れた条件 \(a_{n}+b_{n}+c_{n}=1\) をうまいこと活用して処理していくことも、この分野では必要な力です。 漸化式の処理そのものについては、以下のシリーズも適宜活用してください。 テーマ別演習:漸化式の解法基本パターン 漸化式の解法基本パターン 第1講【2項間漸化式:ズラせば等比数列】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 漸化式は問題を解く中で処理しなければならない場面が多々あります。 確率漸化式などの確率や場合の数の分野との融合 点列など、座標との融合 整数問題との融合 など、漸化式は道具として使う場面が多々あります。 漸化式が立式できても、それが解けないとなると意味がありませんから、基本的な漸化式についてはきちんと処理できる必要があります。 そこで基本的な漸化式について一通りこのシリーズで押さえておきたいと思います このシリーズの一覧はこちら ... 漸化式の解法基本パターン 第2講【2項間漸化式:心霊写真型】 問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 前回の第1講で扱った Type 1 \(a_{n+1}=pa_{n}+q\) ( \(p \neq 1\) ) の派生形として今回は Type 2 (心霊写真型) \(a_{n+1}=pa_{n}+q^{n}\) ( \(p \neq 1\) ) ( \(q\) の肩になんか乗ってる ) というタイプを扱います。 この心霊写真型の除霊の仕方は2パターンあり 心霊写真型の除霊の仕方 ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 漸化式基本パターン第3講では、「分数型」の漸化式を扱います。 まずは分数型の中でも簡単な形(特殊な形)である 分数漸化式(メタボ型) \(a_{n+1}=\displaystyle \frac{ra_{n}}{pa_{n}+q}\) を考えます。 分数の形がなんとなく△の形をしており、引き締まっておりません。 逆数を取ると \(\displaystyle \frac{1}{a_{n+1}}=\disp ... 漸化式の解法基本パターン 第4講【2項間漸化式:特性方程式使うと事故る型】 問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 漸化式の解法基本パターン第4講では 特性方程式使うと事故る型 \(a_{n+1}=pa_{n}+An+B\) というタイプをやっていきます。 長ったらしいネーミングですが、逆に一回事故った方が理解が深まると思います。 (もっといいネーミングがあれば募集します。) 文字のままやっててもピンとこないかもしれませんので、本問の (1) を例にとって、敢えて事故ってみます。 誤答 ... 漸化式の解法基本パターン 第5講【2項間漸化式:そうだ、logをとろう型】 問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 漸化式の解法基本パターン第5講では そうだ、log をとろう型 \(a_{n+1}^{p}=Aa_{n}^{q}\) というタイプを扱います。 両辺底が \(A\) の対数をとると \(p\log_{A}a_{n+1}=q\log_{A}a_{n}+1\) となり、\(b_{n}=\log_{A}a_{n}\) とおくと \(b_{n+1}=\displaystyle \frac{q}{p}b_{n} ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 第6講では「変数倍」型を扱います。 変数倍型 $$a_{n+1}=f(n)a_{n}+A$$ 基本的に\(a_{n+1}=pa_{n}+\cdots\) という「定数倍」であれば、多少のイレギュラーこそあれど、等比数列としての処理に帰着することになります。 今回のように「変数倍」になってくると、形一つで対応が変わってきます。 このあたりを体系的にまとめるのは難しいでしょう。 (1) , (2) は ... 漸化式の解法基本パターン 第7講【隣接3項間漸化式への対応】 問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 第7講では3項間漸化式を扱います。 3項間漸化式 $$a_{n+2}+pa_{n+1}+qa_{n}=0$$ この3項間漸化式の狙い筋は 狙い筋 $$a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_{n})$$ という形に変形することで、等比数列の形として処理することです。 つまり、 \(a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1 ... 漸化式の解法基本パターン 第8講【2種類の連立漸化式への対応】 問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 第8講では「連立漸化式」を扱います。 連立漸化式の代表的な解法としては2つあります。 連立漸化式の代表的方針 1文字消去 上手い倍率を見つけて辺々操作 それぞれについて見てみます。 1文字消去路線について 今回の (1) を例にとってみます。 消しやすい第2式に注目すれば、\(a_{n}=b_{n+1}-b_{n}\) と見ることができます。 第1式に代入するために番号を 1 つ上げれば ... 今回の問題で扱っている2つの関数 \(f_{0}(x)=\displaystyle \frac{x}{2}\) , \(f_{1}(x)=\displaystyle \frac{x+1}{2}\) について考えてみます。 \(f_{0}\) というのは、持ち込まれた \(x\) という値を \(2\) で割る という操作です。 同様に\(f_{1}\) というのは、持ち込まれた \(x\) という値を \(1\) を加えてから、\(2\) で割る という操作です。 「\(2\) で割る」という操作の意味は、\(2\) 進法で考えると明確な意味があり、 2進数表示された数の「小数点を左に1個ずらす」 という意味があります。 普段 \(10\) 進法を使っている我々からすれば、\(10\) で割れば小数点が左に1個ズレるのを想像すればよいでしょう。 では、「\(1\) を加えてから、\(2\) で割る」という操作の意味はどうでしょうか? ぜひ考えてみましょう。 【総括】のあとに【参考】という項目を立ててこのことに触れてあります。この数列の振る舞いをどう捉えるか
\(a_{n+1}=f(a_{n})\) で定まる数列の視覚化
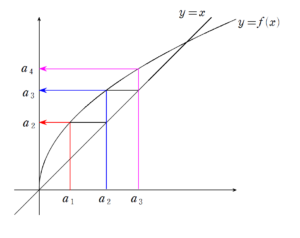
本問の場合
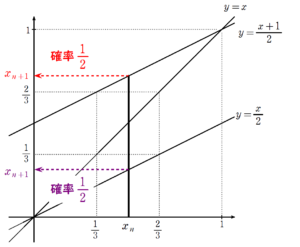
状態推移を視覚化
\(0\lt x_{n} \lt \displaystyle \frac{1}{3}\) からの状態推移

\(\displaystyle \frac{1}{3} \leq x_{n} \lt \displaystyle \frac{2}{3}\) からの状態推移
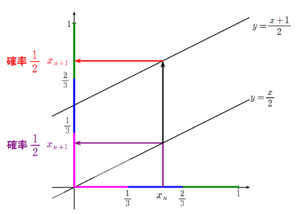
\(\displaystyle \frac{2}{3} \leq x_{n} \lt 1\) からの状態推移
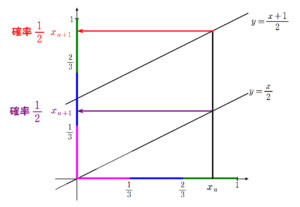
漸化式の立式
\left\{
\begin{array}{l}
a_{n+1} = \displaystyle \frac{1}{2} a_{n}+\displaystyle \frac{1}{2} b_{n} \\
b_{n+1} = \displaystyle \frac{1}{2} a_{n}+\displaystyle \frac{1}{2} c_{n} \\
c_{n+1} = \displaystyle \frac{1}{2} b_{n}+\displaystyle \frac{1}{2} c_{n} \\
\end{array}
\right.
\end{eqnarray}$$本問の操作的意味









