問題はこちら(画像をクリックするとPDFファイルで開きます。)

減衰曲線を扱った定番の問題です。
本問に限らず、同様の趣旨の問題は毎年どこかでは出題されます。
多少の亜種はありますが、シナリオは大きく変わりません。
今回は一番シンプルな \(y=e^{-x}|\sin{x}| \) というタイプの減衰曲線をもってきました。
これについては「定着するまできちんと勉強してきたか」ということで差が付くでしょう。
特に理系の現役生の方は数Ⅲの完成度がモノを言います。
数Ⅲについてはやるべきことや考え方がある程度決まっているので、定番と言える話題についてのシナリオは一通りマスターしておきましょう。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
(1) の定積分の計算は基本です。
難関大受験生でこれを試験場で落とした場合、即死だと思ってください。
ポイント
【 \(\displaystyle \int_{ \ }^{ \ } e^{\theta}\sin \theta d\theta\) , \(\displaystyle \int_{ \ }^{ \ } e^{\theta}\cos \theta d\theta\) の処理 】
「部分積分からの同形出現」
または
「\((e^{\theta}\sin \theta)' , (e^{\theta}\cos \theta)'\) の辺々操作」
によって処理するのが常套手段です。
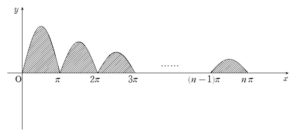
(2) についてはまず今回の定積分が表す面積がどこなのかを図示しましょう。

ガッツリ微分して増減表を書いて \(\cdots\) までしなくても、\(\sin{ \ }\) なので基本は波の形で、振幅に相当する部分が単調減少の \(e^{-x}\) なので段々振れ幅が小さくなっていくなというぐらいの外観で大丈夫です。
ここで、\(a_{k}=\displaystyle \int_{(k-1)\pi}^{ k\pi } e^{-x}|\sin{x}| dx\) と、\(k\) 番目の山の面積を \(a_{k}\) とします。
\(\displaystyle \int_{0}^{ n\pi } e^{-x}|\sin{x}| dx=a_{1}+a_{2}+\cdots+a_{n}\) となりますので、一般項 \(a_{k}\) を求めてその和を出す流れです。
この \(a_{k}\) を求めるにあたっては
減衰曲線の計算のカギ
【方法1】積分区間を簡単にする置換積分
【方法2】\((k-1)\pi \leq x \leq k\pi\) において \(| \sin{x}|=(-1)^{k-1}\sin{x}\) として処理する
という2路線あります。
足腰を鍛えるという点で、2路線実際に手を動かすことで確認してもらいたいですが、実戦の現場では【方法1】がよく用いられると思います。
その反面【方法1】は「知らなきゃ厳しい」という置換積分ですので、初見の方であれば、今後の糧にできればそれでよしだと思います。
また、この減衰曲線は至る所に等比数列が現れます。
今回の数列 \(\{a_{k}\}\) も実は等比数列です。
それなりに計算が煩雑になりますから、等比数列になるという結果が分かっているだけでも、精神的にはいくらか楽になる部分があると思います。
解答はコチラ