例題はこちら(画像をクリックするとPDFファイルで開きます。)
類題はこちら(画像をクリックするとPDFファイルで開きます。)
条件付き確率についての基本演習問題です。
条件付き確率の基本的なイメージを掴むとともに、何を求めるべきなのかをしっかりと芯でとらえられるようになりましょう。
本問は古い問題ですが、最近の教科書傍用問題集や網羅系参考書などにも収録されている条件付き確率に関する古き良き名作です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 事象 \(A\) が起こったという条件の下で、事象 \(B\) が起こるという条件付き確率を \(P_{A}(B)\) と表します。 \(A\) が起こったということが確定すれば、全事象(可能性)は \(n(A)\) ということになり、その中で \(B\) が起こる確率が \(P_{A}(B)\) ということですから、 \(P_{A}(B)=\displaystyle \frac{n(A \cap B)}{n(A)}\) となります。 この分母分子を \(n(U)\) で割ることで \(P_{A}(B)=\displaystyle \frac{P(A \cap B)}{P(A)}\) ということが言えます。 通常の確率と条件付き確率の違いは 情報が入ることにより、全事象(可能性の数)が縮む という点にあります。 何も情報がなければ、全事象の総数(可能性の数)は \(n(U)\) なのですが、 事象 \(A\) が起こった という情報が入る(条件が付く)ことにより、余計な可能性が減るわけです。 \(P_{A}(B)=\displaystyle \frac{P(A \cap B)}{P(A)}\) の分母を払うと \(P(A \cap B)=P(A) \cdot P_{A}(B)\) ということになります。 この右辺は ということで、これが左辺の \(A\) が起こり、かつ \(B\) が起こる確率 となっているのは分かりやすい形と言えましょう。 この分母を払った形が分かりやすい一つの理由は という部分にあるでしょう。 本問は 「帽子を忘れてしまった」 という結果に対して、それが 「\(\mathrm{B}\) の家に忘れたことが原因である確率は?」 という「原因の確率」です。 基本的には 理由 → 結果 というように、何か理由があり、それに起因して結果が起こるというのが通常の時系列です。 起こってしまった結果に対して、その原因の確率を考えるのは時系列を遡ることになるため、この条件付き確率 \(P_{A}(B)=\displaystyle \frac{P(A \cap B)}{P(A)}\) を用いて捌くわけです。 慣れてくればどうってことはありませんが、 「確率を確率で割る」 というのがピンとこない人は、 神様を登場させ、神様がくじを引くことでその人の行動が決まる という考え方を導入することで、場合の数を場合の数で割るという通常の組合せ論的確率の方で考えられなくもありません。 それについては【総括】の方で少し触れてあります。 何も条件がなければ、3人の証言は のようにバラバラになるものも含めて、全事象の可能性は沢山あります。 それが 3人とも「表」と証言した という情報が入ることにより、全事象が縮むわけで、条件付き確率の問題となるわけです。条件付き確率の定義とイメージ
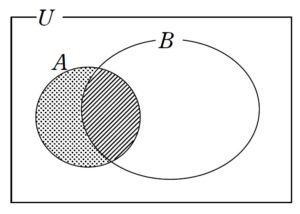
条件付き確率のイメージ
分母を払うと

本問について
例題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
類題について
類題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)


