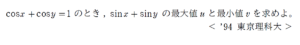問題はこちら(画像をクリックするとPDFファイルで開きます。)
見かけ上、従属2変数関数の最大・最小問題に見えます。
実際には、薄皮一枚剥ぐと、「三角関数の連立方程式の運用」という部分がメインの処理内容になります。
路線によってはウルサイことになりかねないので、解法の検討という部分も勉強の内容に含まれるテーマです。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 従属2変数関数の最大最小問題に対する最有力候補は 文字消去 です。 ただし今回の場合、裸の変数ではなく、三角関数の服をきているため、一見すると文字消去が困難です。 文字消去が困難な場合の次なる有力手段は 逆像法 です。 この逆像法の使いどころや考え方については テーマ別演習:逆像法 逆像法 第1講【逆像法の考え方と使いどころをマスター】【最大最小問題への応用】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 今回は難関大を目指すにあたっては避けて通れない話題である「逆像法」について扱います。 このシリーズを通じて 逆像法のもつイメージ 逆像法の代表的な使いどころ をマスターし、状況に応じて自分で使いこなせるようにすることでライバルに差をつけましょう。 このシリーズの一覧はこちら 代表的な使いどころ 入試によく出題される話題の中で、逆像法が有効にはたらく場面というのは以下の話題です。 逆像法の代表的な使いどころ 最大最小問題への応用 ... 逆像法 第2講【座標変換への応用】【線形計画法の考え方の素】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 逆像法シリーズの第2講は 座標変換への応用 線形計画法 と逆像法についての関連を見ていきます。 このシリーズの一覧はこちら (以下ネタバレ注意) + クリック(タップ)して続きを読む (1) について \((x \ , \ y)\) という座標から \((x+y \ , \ xy)\) という座標への変換を考える問題です。 1954年に東大が出題したのが元祖で、通称「エンマさまの唇問題」と呼ばれている ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) 逆像法シリーズ第3講は 通過領域 という難関大入試でも頻出の話題について扱います。 このシリーズの一覧はこちら (以下ネタバレ注意) + クリック(タップ)して続きを読む 直接目で追いきれないので \(\cdots\) 今回、\(a\) が動くにつれて円 \(C_{a}\) も動くわけですが、中心、半径が同時に動くため、ラフな動きはともかく、細かな動きを目で追いきることは難しいでしょう。 そこで、逆に ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) 逆像法第4講は 方程式の実数解がとり得る値の範囲 を考えるにあたって、逆像法が活用できるということを見ていきます。 このシリーズの一覧はこちら (以下ネタバレ注意) + クリック(タップ)して続きを読む (1) について これについては2次方程式の解に関する注文が入ってくる、いわゆる「解の配置問題」です。 整理しないとグチャグチャになりやすいタイプだと思います。 \(x=0\) を解にもつとき \(x=2\) を解 ... にて詳しく解説しています。 本問においては、\(\sin{x}+\sin{y}=k\) とおき、 どんな \(k\) なら実現可能か を考えます。 これにより $$\begin{eqnarray} を同時に満たすことができるような \(k\) の条件を求めることになります。 つまりは、この連立方程式が実数解をもつかどうかという問題になります。 ですから、 \(\cos^{2}{y}+\sin^{2}{y}=1\) に代入することにより、 \((1-\cos{x})^{2}+(k-\sin{x})^{2}=1\) と、\(y\) を消去することができます。 これを整理すると \(k\sin{x}+\cos{x}=\displaystyle \frac{k^{2}+1}{2}\) すなわち \(\sqrt{k^{2}+1}\sin{(x+\alpha)}=\displaystyle \frac{k^{2}+1}{2}\) \(\sin{(x+\alpha)}=\displaystyle \frac{\sqrt{k^{2}+1}}{2}\) ということになります。 ※ \(\alpha\) は $$\begin{eqnarray} を満たしています。 これを満たす \(x\) が存在すればよいので、 \(\displaystyle \frac{\sqrt{k^{2}+1}}{2} \leq 1\) ということになり、ここから \(-\sqrt{3} \leq k \leq \sqrt{3}\) を得て解決します。 経験がモノを言う見方をすることは否めませんが、 $$\begin{eqnarray} という関係式を $$\left( とベクトルの和として見てやります。 これにより、視覚的に \(k\) の範囲を求めることも可能です。 この路線については【解2】で解説しています。 $$\begin{eqnarray} という関係式から $$\begin{eqnarray} と辺々2乗して加えると \(1+2 \cos{(x-y)}+1=1+k^{2}\) から、 \(\cos{(x-y)}=\displaystyle \frac{k^{2}-1}{2}\) を得ることを考える人も多いでしょう。 ここから \(-1 \leq \displaystyle \frac{k^{2}-1}{2} \leq 1\) として \(-\sqrt{3} \leq k \leq \sqrt{3}\) を得られます。 ただ、この方針の場合、2乗することによって同値性が崩れてしまいます。 注意
①:\(2x-1=3\) を満たす \(x\) 集まれ~ と呼びかけて集まってくる \(x\) と ②:\((2x-1)^{2}=9\) を満たす \(x\) 集まれ~ と呼びかけて集まってくる \(x\) は違います。 ② の呼びかけで集まってきた \(x\) が ① を満たしている保証がありません。 したがって、必要性と十分性について論じなければなりません。 このあたりがウルサイので、できればこの路線は避けたいというのが本音です。 ただ、そもそも同値性が崩れていることを気に留めない受験生も多いでしょう。 一応、今回は「こんなめんどいことになりまっせ」ということで【解3】で触れてあります。文字消去困難なときの有力手段
\left\{
\begin{array}{l}
\cos{x}+\cos{y}=1 \\
\sin{x}+\sin{y}=k
\end{array}
\right.
\end{eqnarray}$$方針1:今度こそ文字消去
\left\{
\begin{array}{l}
\cos{\alpha}=\displaystyle \frac{k}{\sqrt{k^{2}+1}} \\
\sin{\alpha}=\displaystyle \frac{1}{\sqrt{k^{2}+1}}
\end{array}
\right.
\end{eqnarray}$$方針2:視覚化する
\left\{
\begin{array}{l}
\cos{x}+\cos{y}=1 \\
\sin{x}+\sin{y}=k
\end{array}
\right.
\end{eqnarray}$$
\begin{array}{c}
\cos{x} \\
\sin{x}
\end{array}
\right)+\left(
\begin{array}{c}
\cos{y} \\
\sin{y}
\end{array}
\right)=\left(
\begin{array}{c}
1 \\
k
\end{array}
\right)$$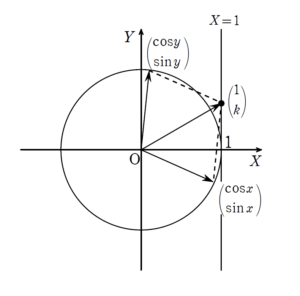
方針3:辺々2乗する
\left\{
\begin{array}{l}
\cos{x}+\cos{y}=1 \\
\sin{x}+\sin{y}=k
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
\cos^{2}{x}+2 \cos{x}\cos{y}+\cos^{2}{y}=1 \\
\sin^{2}{x}+2 \sin{x}\sin{y}+\sin^{2}{y}=k^{2}
\end{array}
\right.
\end{eqnarray}$$