例題はこちら(画像をクリックするとPDFファイルで開きます。)
コッホ雪片と呼ばれる有名な図形を題材とした問題です。
操作の意味と特徴をしっかりと把握できれば、問題の難易度自体は標準的な難易度です。
(以下ネタバレ注意)
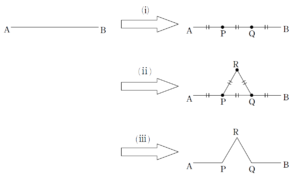
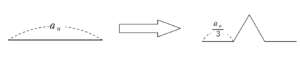
+ クリック(タップ)して続きを読む 今回の操作は というように、外側に「ボコ」っと盛り上がるようなイメージです。 今回の図形 \(D_{0}\) , \(D_{1}\) , \(D_{2}\) \(\cdots\) のイメージは というように変化していきます。 操作を重ねるにつれ、雪の結晶のような形に近づいていくため「コッホ雪片」と呼ばれています。 一本の線分に対して今回の操作を繰り返していったものは「コッホ曲線」と呼ばれ、 というように、拡大しても拡大しても同様の構造が現れるという 自己相似構造 をもっており、フラクタル図形と呼ばれます。 イメージでいうと、マトリョーシカのようなイメージでしょうか。 \(D_{n}\) の1辺の長さを \(a_{n}\)、辺の本数を \(b_{n}\) とします。 \(L_{n}=a_{n}b_{n}\) であるため、 \(a_{n}\) , \(b_{n}\) が把握できれば勝負ありです。 \(D_{n+1}\) の1辺の長さ \(a_{n+1}\) について というように、変化しますから \(a_{n+1}=\displaystyle \frac{1}{3}a_{n}\) という漸化式が立ち、数列 \(\{a_{n}\}\) は初項 \(a\) , 公比 \(\displaystyle \frac{1}{3}\) の等比数列ということになります。 よって、一般項 \(a_{n}\) は \(a_{n}=a \cdot (\displaystyle \frac{1}{3})^{n} \ (n=0 \ , \ 1 \ , \ 2 \ , \ \cdots)\) と得られることになります。 辺の本数は 1辺が4本の折れ線に変化する ということから \(b_{n+1}=4b_{n}\) という漸化式が立ちます。 よって、一般項 \(b_{n}\) は \(b_{n}=3 \cdot 4^{n} \ (n=0 \ , \ 1 \ , \ 2 \ , \ \cdots)\) と得られることになります。 \(D_{n}\)の面積 \(S_{n}\) に対して、 \(S_{n+1}=S_{n}+(増加分)\) というイメージが立つでしょう。 最終的にはこの「増加分」を把握し、階差数列としての処理をすることで \(S_{n}\) を Get します。 この増加分は 1辺の長さが \(a_{n+1}\) の正三角形が \(b_{n}\) 個分 です。 (3) の極限については、\(S_{n}\) が出ていればボーナス問題です。 詳しい計算結果は【解答】で計算していますが、 となります。 このことから、 というように、 という結果を得ます。 無限に長い周の長さが有限のエリアに収められているという、直感的には不思議な結果です。 長~いものが限られたエリアに収まるというのは、ある意味価値ある結果と見ることもできるでしょう。 コッホ図形では正三角形を外側に追加していきましたが、 正方形だとどうでしょう という内容です。 この場合、追加分がゴッツンコして隙間がうまれる可能性もあります。 そのあたりに関しても話題にしながら問いにしていたり、オチの問題についても結局何がいえればよいのかを考えさせるスッキリするオチです。今回の操作
今回の図形のイメージ
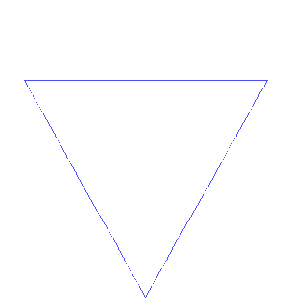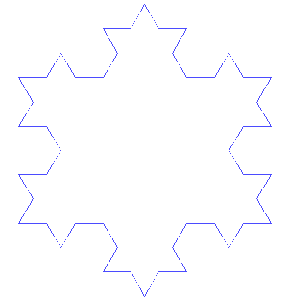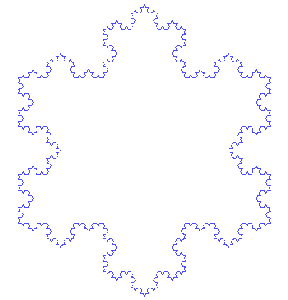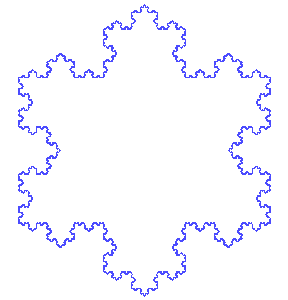
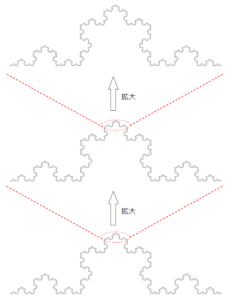
周の長さについて
\(a_{n}\) について
\(b_{n}\) について
面積について
今回の結果
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)


