例題はこちら(画像をクリックするとPDFファイルで開きます。)
イェンゼンの不等式と呼ばれる有名な不等式に関する証明問題です。
例題は具体的な関数で、文字数が
- (1) 2文字&2文字
- (2) 3文字&3文字
という具体的な例です。
それにしてもアタフタする受験生は多いと思います。
初見殺しの要素は存分にありますから、ひとまずは要領を例題でつかむことを目的としてください。
有名テーマなので、初見でできなくても自信を失う必要はありません。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む イェンゼンの不等式とは次のような「凸性」をもった関数に関する不等式です。 イェンゼンの不等式 ある区間において \(f''(x) \gt 0\) を満たす関数 \(f(x)\) について考える。 \(p_{1}+p_{2}+\cdots+p_{n}=1\) を満たす \(0\) 以上の実数 \(p_{k}\) ( \(k=1 \ , \ 2 \ , \ \cdots \ , \ n \) ) 及び区間内の任意の \(x_{1}\) , \(x_{2}\) , \(\cdots\) , \(x_{n}\) に対して が成り立つ。 なお、\(f''(x) \lt 0\) , すなわち \(f(x)\) が上に凸の場合は不等号の向きが反対になります。 まず、本問は \(f(x)=\log{x}\) という上に凸の関数です。 (1) はイェンゼンの不等式における \(n=2\) のときの証明です。 方針としては2路線あります。 凸性を利用して視覚化することで不等式を目で見て示す方針が考えられます。 ただ、見えるか見えないかの一発系の路線で、その見えるか見えないかについては経験がモノを言う部分が大きいでしょう。 \(\mathrm{A}(x \ , \ \log{x})\) , \(\mathrm{B}(y \ , \ \log{y})\) という2点 \(\mathrm{A}\) , \(\mathrm{B}\) に対し、線分 \(\mathrm{AB}\) を \(b : a\) に内分する点 \(\mathrm{C}\) を考えると \(\mathrm{C}(\displaystyle \frac{ax+by}{b+a} \ , \ \displaystyle \frac{a\log{x}+b\log{y}}{b+a})\) \(a+b=1\) という条件から \(\mathrm{C}(ax+by \ , \ \ a\log{x}+b\log{y})\) となります。 視覚化が見えなかった場合、差を取って微分することで証明するという腕力路線もあります。 ただ、文字が多く、 と、異なる関係性ですから、それ相応の態度で扱いましょう。 この路線は【解2】で扱っています。 \(y=\log{x}\) に対するイェンゼンの不等式の \(n=3\) のときの証明です。 ここでも方針は2路線あります。 3つの和 \(a+b+c=1\) を \((a+b)+c=1\) と2つの和として見ることで、(1) の結果を利用してやる路線があります。 この路線は という流れで、ここで用いる考え方や要領をマスターできれば \( \ \ \ \ \ \ \vdots\) と一般論に拡張できます。 ここまで言えば分かると思いますが、イェンゼンの不等式の証明としては数学的帰納法が有力手段となります。 視覚化という路線で倒すこともできます。 \(a+b+c=1\) という設定をうまく図形的に利用するために、(1) でも考えた 内分点公式 の活用を考え付きたいところです。 (1) では「座標に対する内分点公式」を用いて一気に視覚化しましたが、今回は3文字あるので一気に処理しようとすると混乱すると思います。 そこで、「ベクトルに対する内分点公式」と見て処理していきます。 この路線については【解3】で扱っています。 ただ、(1) ではメイン方針であった視覚化ですが、一般論への拡張ということを考えると、(2) に関しては方針1の方が汎用性がある自然な路線でしょう。 下に凸の場合の一般論の証明です。 例題で \(n=2\) から \(n=3\) へ橋渡しした際の要領が身についていれば、同じ要領で帰納法の橋渡しが完成するはずです。 なお、イェンゼンの不等式をネタにしたと思われる入試問題は数多くありますが、証明なしに用いてよいかどうかという部分については「使うなら減点覚悟の自己責任」でお願いします。 問題作成側はネタ元として利用することはあると思いますが、(多くの)受験生の解答としてイェンゼンの不等式を用いた解答を期待しているとは思えません。 誘導設問などが付いていた場合、出題者側がやらせたいことはそこから読み取れると思います。イェンゼンの不等式とは
(1) について
方針1:視覚化
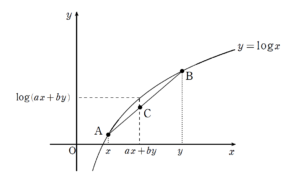
方針2:式でゴリゴリ証明する
(2) について
方針1:(1) の結果を利用する。
方針2:視覚化する
一般論について
一般論の証明はこちら(画像をクリックするとPDFファイルで開きます。)


