問題はこちら(画像をクリックするとPDFファイルで開きます。)
これ1題で
重心・垂心・外心・内心の位置ベクトル
の導出について学べるめちゃくちゃコスパの良い問題です。
三角形の代表的な点の位置ベクトルについての基本的な理解を確認するとともに、その特徴を活かして自力で導出できることを本問の目標としたいと思います。
この数字設定は解き進めていくと、
「めんどくさっ」
と思えてきますが、反面
「これ狙って作ったとしたらすげぇな」
というちょっとした驚きも含まれており、この話題をマスターしている人も確認のために一度自分の手で計算してみると楽しめると思います。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 今回主役となる基底 \(\vec{a}\) , \(\vec{b}\) に関する情報である \(|\vec{a}|\) , \(|\vec{b}|\) , \(\vec{a} \cdot \vec{b}\) を先に計算しておきます。 \(|\vec{a}|\) , \(|\vec{b}|\) については \(|\vec{a}|=13\) , \(|\vec{b}|=15\) と即 Get できます。 内積 \(\vec{a} \cdot \vec{b}\) については \(|\overrightarrow{\mathrm{BA}}|^{2}=14^{2}\) すなわち \(|\vec{a}-\vec{b}|^{2}=14^{2}\) を2乗展開して得られる \(|\vec{a}|^{2}-2 \vec{a} \cdot \vec{b}+|\vec{b}|^{2}=14^{2}\) から求めることができ , \(\vec{a} \cdot \vec{b}=99\) と求まります。 まとめると となります。 今回は3辺が分かっているから という流れを取る人もいるかと思いますが、 ベクトルの2乗展開と余弦定理は本質的には同じことを意味する ということは押さえておきたいところです。 なぜそんなことが言えるのか納得したかったら 余弦定理をベクトルの言葉で書き換えてみる のが一番です。 本問を例にとって考えてみます。 \(\overrightarrow{\mathrm{CA}}\) , \(\overrightarrow{\mathrm{CB}}\) のなす角を \(\theta\) とすると これは となっています。 つまり、余弦定理をベクトル語でかけば、あたかもそれは「2乗展開」しているように見えるわけです。 逆に言えば、ベクトルの世界で2乗展開をするということは ということになります。 重心については公式一発です。 今回で言えば となり、 \(\overrightarrow{\mathrm{CG}}=\displaystyle \frac{1}{3} \vec{a}+\displaystyle \frac{1}{3} \vec{b}\) と、即解決です。 \(\overrightarrow{\mathrm{CH}}=s\vec{a}+t\vec{b}\) と実数 \(s\) , \(t\) で置くところから始めます。 垂心の性質から $$\begin{eqnarray} ということが言えますが、実際にはどれか 2 つを言えば十分です。 どれでもいいというのであれば、 $$\begin{eqnarray} として処理したいと思うのが通常の感覚だと思います。 できる限り展開作業は楽な方がいいですからね。 これも \(\overrightarrow{\mathrm{CO}}=p\vec{a}+q\vec{b}\) などと、置くところからスタートします。 \(\triangle{\mathrm{ABC}}\) の外心は \(\triangle{\mathrm{ABC}}\) の各辺の垂直二等分線の交点 として得られる点です。 ただ、これも垂心同様 どれか2本の垂直二等分線の交点 として処理すれば十分です。 そこで、線分 \(\mathrm{CA}\) , \(\mathrm{CB}\) の中点をそれぞれ \(\mathrm{M}\) , \(\mathrm{N}\) とします。 すると となります。 これにより、\(\overrightarrow{\mathrm{MO}}\) , \(\overrightarrow{\mathrm{NO}}\) が主役の2本 \(\vec{a}\) , \(\vec{b}\) で表せましたから、あとは $$\begin{eqnarray} として処理すればよいでしょう。 内心は 三角形の内角の二等分線の交点 として得られる点です。 内角の二等分線の性質である によって , 内分比を順次求めていきながら進めていきます。 垂心と外心の導出過程は \(〇\vec{a}+□ \vec{b}\) などと 文字で置いてから、話を進めていく という態度です。 内分比などを読み取りながら、ベクトルを 繋いだり、縮めたりして話を進めていく という態度です。 補足注意
外心の場合 \(|\overrightarrow{\mathrm{OA}}|=|\overrightarrow{\mathrm{OB}}|=|\overrightarrow{\mathrm{OC}}|\) として処理していく方針も目につくかもしれません。 これでもいけないことはありませんが、位置ベクトルを求めるだけであれば、先述した方法の方が個人的には楽に感じます。 もちろん、問題によっては \(|\overrightarrow{\mathrm{OA}}|=|\overrightarrow{\mathrm{OB}}|=|\overrightarrow{\mathrm{OC}}|\) を存分に活かしながら解き進める問題もありますので、臨機応変に対応しましょう。 冒頭述べたちょっとしたサプライズについては、【総括】のあと「余談」で触れてあります。主役(基底)の情報の用意

補足:ベクトルの2乗展開と余弦定理

重心の位置ベクトルについて
垂心の位置ベクトルについて
\left\{
\begin{array}{l}
\overrightarrow{\mathrm{BH}} \cdot \vec{a}=0 \\
\overrightarrow{\mathrm{AH}} \cdot \vec{b}=0 \\
\overrightarrow{\mathrm{CH}} \cdot \overrightarrow{\mathrm{AB}}=0
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
\overrightarrow{\mathrm{BH}} \cdot \vec{a}=0 \\
\overrightarrow{\mathrm{AH}} \cdot \vec{b}=0
\end{array}
\right.
\end{eqnarray}$$外心の位置ベクトルについて
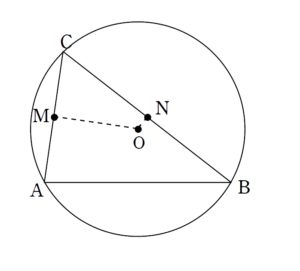
\left\{
\begin{array}{l}
\overrightarrow{\mathrm{MO}} \cdot \vec{a}=0 \\
\overrightarrow{\mathrm{NO}} \cdot \vec{b}=0
\end{array}
\right.
\end{eqnarray}$$内心の位置ベクトルについて
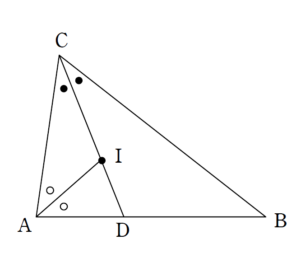
態度の違い
垂心と外心の導出過程
内心の導出過程

