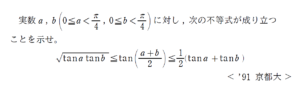問題はこちら(画像をクリックするとPDFファイルで開きます。)
\(\mathrm{tan}\) に関する不等式証明であり、「平均値の代入値」が \(\tan{a}\) と \(\tan{b}\) の相加平均と相乗平均の間に挟まれることを示させる問題です。
相加平均や相乗平均などの意味のある形の式が登場するため、目を引く主張ですね。
京大受験生であれば、右側の不等式については何らかの形で捌いてほしいとは思います。
難しいのは左側の不等式の証明で、何かしらの切れ味が求められます。
ただ、その発想は突拍子もないものではなく、聞いてしまえばちょっとしたアイデアです。
そのあたりのセンスを試す京大らしい問題だと思います。
(以下ネタバレ注意)
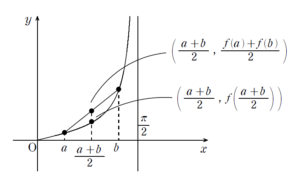
+ クリック(タップ)して続きを読む それなりに学習を進めていれば、示すべき不等式の右側の形は 凸性の利用 を彷彿とさせる形だと感じるでしょう。 \(f(x)=\tan{x}\) について、\(f(x)\) が下に凸の関数であることを考えると \(f(\displaystyle \frac{a+b}{2}) \leq \displaystyle \frac{f(a)+f(b)}{2}\) すなわち \(\tan{\displaystyle \frac{a+b}{2}} \leq \displaystyle \frac{\tan{a}+\tan{b}}{2}\) ということになり、証明完了です。 なお、この凸性を利用した不等式証明については 例題はこちら(画像をクリックするとPDFファイルで開きます。) イェンゼンの不等式と呼ばれる有名な不等式に関する証明問題です。 例題は具体的な関数で、文字数が (1) 2文字&2文字 (2) 3文字& ... 続きを見る でしっかり取り扱っています。 凸性の利用を思いつかなかった場合、独立2変数の扱いの最有力手段の一つである 予選決勝法 を用いることを思いつく人もいて当然です。 差を取ったものを \(f(a)=\displaystyle \frac{1}{2}(\tan{a}+\tan{b})-\tan{\displaystyle \frac{a+b}{2}}\) というように、\(b\) を固定し、\(a\) の関数と見ます。 この路線については【解2】で扱っています。 加法定理や2倍角の公式、半角の公式を使うことを考えた場合、\(\displaystyle \frac{a+b}{2}\) という角度が鬱陶しいので \(\displaystyle \frac{a+b}{2}=\alpha\) などと置いてしまい、\(\displaystyle \frac{a-b}{2}=\beta\) と設定することで \(a=\alpha+\beta\) , \(b=\alpha-\beta\) と、目に優しい形で加法定理を使うことができます。 これにより、愚直に差を取るという方針が現実味を帯びてきます。 ただし、この置き換えに辿り着くのは決して簡単ではないでしょう。 この路線は【解4】で扱っています。 示すべき不等式の左側の不等式の両辺は \(0\) 以上の値であるため \(\tan{a} \tan{b} \leq (\tan{\displaystyle \frac{a+b}{2}})^{2}\) を示せばよいわけです。 \(f(a)=(\tan{\displaystyle \frac{a+b}{2}})^{2}-\tan{a} \tan{b}\) と \(a\) の関数と見て予選決勝法で進めてみると \(\begin{eqnarray} となり、このあたりでテンションが下がってくると思います。 方針としては ①:証明済みの右側の不等式の活用【解1】 ②:上述の置き換え路線【解4】 ③:凸性の利用【解3】 が考えられます。 ③ の凸性の利用については、根号を捌くために \(\mathrm{log}\) をとると見えてきますが、そのように見るのは容易ではないでしょう。 冒頭述べたように、何かしら山場があるため、完答するためには確かな力が必要であり、完答できれば自信をもってよい問題でしょう。右側の不等式について
路線1:凸性を利用する

参考イェンゼンの不等式【証明】【2003年度 和歌山県立医科大学ほか】
路線2:予選決勝法
路線3:置き換え
左側の不等式について
予選決勝法では \(\cdots\)
f'(a) &=& 2 (\tan{\displaystyle \frac{a+b}{2}}) \cdot \displaystyle \frac{1}{\cos^{2}(\displaystyle \frac{a+b}{2})} \cdot \displaystyle \frac{1}{2}-\tan{b} \cdot \displaystyle \frac{1}{\cos^{2}{a}} \\
&=& \tan{\displaystyle \frac{a+b}{2}}(1+\tan^{2}{\displaystyle \frac{a+b}{2}})-\tan{b}(1+\tan^{2}{a})
\end{eqnarray}\)