問題はこちら(画像をクリックするとPDFファイルで開きます。)
円を折り返したときの折り目の存在範囲を考える問題です。
シンプルな題意ですが、解き進めていくといくつかの上級テーマが次から次へと襲い掛かってくるため、完答するためにはそれらを払いのけるだけの確固たる力が必要です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む まずは座標の設定です。 自然に設定するとしたら \(\mathrm{A}\)\((-1 \ , \ 0)\) , \(\mathrm{B}\)\((1 \ , \ 0)\) と設定し、接点を \(\mathrm{T}\)\((t \ , \ 0)\) とします。 もちろん、この \(t\) は \(-1 \leq t \leq 1\) として設定します。 ひとまずの目標は 直線 \(\mathrm{PQ}\) の方程式を Get すること です。 そうなってくると のように、折り返した円弧の全体像を復元し、 2円の交点を通る直線 として求めればよいでしょう。 元々の半円 (上図における \(C\)) は \(x^{2}+y^{2}=1\) と即答です。 また、折り返した円弧の全体像の円 (上図における \(C'\)) は であることを考えると ポイント \(C\) , \(C'\) の半径は等しい ということが言えます。 \(C'\) は \(x\) 軸に接しているということも考えると \((x-t)^{2}+(y-1)^{2}=1\) と、円 \(C'\) が表す方程式が得られます。 円 \(C\) , \(C'\) の交点を通る直線は $$\begin{eqnarray} の辺々を引いて得られる \(2tx+2y-t^{2}-1=0\) として得られます。 これが目標の直線 \(\mathrm{PQ}\) の方程式ということになります。 交点に直接触れずに「交点を通る図形」を立式するスキルについては 問題はこちら(画像をクリックするとPDFファイルで開きます。) 放物線の交点によってできる四角形の対角線の方程式を求めるという問題です。 まともにカチ合うと茨の道であることは目に見えると思います。 テ ... 続きを見る などで解説しています。 直線 \(\mathrm{PQ}\) の式が得られたら、次は \(t\) を \(-1 \leq t \leq 1\) の範囲で動かしたときの 線分 \(\mathrm{PQ}\) の通過領域 を求めることに目がいくことになります。 ただ、線分の通過領域については範囲的なものもあり、まともにぶつかると厄介なことになります。 そこで一旦 直線 \(\mathrm{PQ}\) の通過領域 を求め、そのうち $$\begin{eqnarray} という 半円の内部 としてとらえるのが得策です。 直線の通過領域については様々な解法が考えられますが、今回は 逆像法 で倒します。 逆像法については 逆像法 第1講【逆像法の考え方と使いどころをマスター】【最大最小問題への応用】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 今回は難関大を目指すにあたっては避けて通れない話題である「逆像法」について扱います。 このシリーズを通じて 逆像法のもつイメージ 逆像法の代表的な使いどころ をマスターし、状況に応じて自分で使いこなせるようにすることでライバルに差をつけましょう。 このシリーズの一覧はこちら 代表的な使いどころ 入試によく出題される話題の中で、逆像法が有効にはたらく場面というのは以下の話題です。 逆像法の代表的な使いどころ 最大最小問題への応用 ... 逆像法 第2講【座標変換への応用】【線形計画法の考え方の素】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 逆像法シリーズの第2講は 座標変換への応用 線形計画法 と逆像法についての関連を見ていきます。 このシリーズの一覧はこちら (以下ネタバレ注意) + クリック(タップ)して続きを読む (1) について \((x \ , \ y)\) という座標から \((x+y \ , \ xy)\) という座標への変換を考える問題です。 1954年に東大が出題したのが元祖で、通称「エンマさまの唇問題」と呼ばれている ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) 逆像法シリーズ第3講は 通過領域 という難関大入試でも頻出の話題について扱います。 このシリーズの一覧はこちら (以下ネタバレ注意) + クリック(タップ)して続きを読む 直接目で追いきれないので \(\cdots\) 今回、\(a\) が動くにつれて円 \(C_{a}\) も動くわけですが、中心、半径が同時に動くため、ラフな動きはともかく、細かな動きを目で追いきることは難しいでしょう。 そこで、逆に ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) 逆像法第4講は 方程式の実数解がとり得る値の範囲 を考えるにあたって、逆像法が活用できるということを見ていきます。 このシリーズの一覧はこちら (以下ネタバレ注意) + クリック(タップ)して続きを読む (1) について これについては2次方程式の解に関する注文が入ってくる、いわゆる「解の配置問題」です。 整理しないとグチャグチャになりやすいタイプだと思います。 \(x=0\) を解にもつとき \(x=2\) を解 ... を参考にしてください。 また、線分の通過領域について場数を踏みたい方は 問題はこちら(画像をクリックするとPDFファイルで開きます。) 難関大頻出の話題である「通過領域」の問題の中でも、一番シンプルな「直線の通過領域」について考えます。 さらに、その延長にある「線分の通過 ... 続きを見る 問題はこちら(画像をクリックするとPDFファイルで開きます。) 円と円の交点を結ぶ線分の通過領域を求める問題です。 円 \(C\) は固定されていますが、円 \(C'\) の動きは点 \((1 \ , ... 続きを見る なども活用してみてください。 \((X \ , \ Y)\) が直線 \(\mathrm{PQ}\) の通過領域に含まれる点かどうかについては、 \(2tX+2Y-t^{2}-1=0\) を満たすように \(t\) を仕組めるかどうかが問題です。 つまり、 \(t\) の2次方程式 \(t^{2}-2Xt-2Y+1=0\) が \(-1 \leq t \leq 1\) の範囲に少なくとも 1 つ実数解をもつ となるような \(X\) , \(Y\) の条件について考えることになります。 2次方程式の解に関して注文が入る問題は俗に「解の配置」と言われ、その中でも 「少なくとも1つ~~」 というタイプは少々鬱陶しいタイプです。 このあたりでアタフタしないためには、ある程度「少なくとも1つ型」の解の配置問題について手際よく捌けるだけの練習を積んでおきたいところです。 それについては 例題はこちら(画像をクリックするとPDFファイルで開きます。) 2次方程式の解に関して注文が入る「解の配置問題」と呼ばれる問題です。 その中でも今回扱うのは 「少なくとも1つ」 というタイプです。 こ ... 続きを見る などで場数を踏んでみてほしいと思います。座標の設定
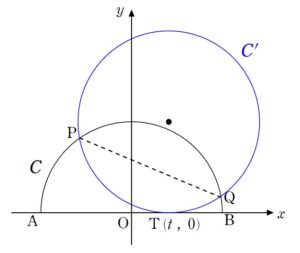
2円の交点を通る直線
\left\{
\begin{array}{l}
x^{2}+y^{2}-1=0 \\
x^{2}+y^{2}-2tx-2y+t^{2}=0
\end{array}
\right.
\end{eqnarray}$$

参考放物線の交点による四角形の対角線【2011年度 立命館大学】
線分の通過領域
\left\{
\begin{array}{l}
x^{2}+y^{2} \leq 1 \\
y \geq 0
\end{array}
\right.
\end{eqnarray}$$

参考直線の通過領域、線分の通過領域【2009年度 横浜国立大学】

参考2円の弦の通過領域【2円の交点を結ぶ線分】【1994年度 東京都立大学】
解の配置

参考解の配置問題【左辺と右辺の組み換え】【2003年度 大阪市立大学ほか】