(1) について
\(\alpha\)が鋭角なのであれば

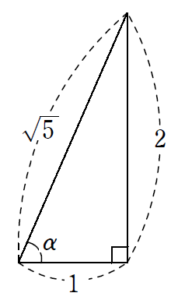
という図を考えれば、
\(\sin{\alpha}=\displaystyle \frac{2}{\sqrt{5}}\)
と即求まります。
(2) について
\(\tan{ \ }\) についての加法定理
\(\tan(\theta_{1}+\theta_{2})=\displaystyle \frac{\tan{\theta_{1}}+\tan{\theta_{2}}}{1-\tan{\theta_{1}}\tan{\theta_{2}}}\)
を順次用いていけばよいでしょう。
$$\begin{eqnarray}
\tan(\alpha+\beta+\gamma)&=& \displaystyle \frac{\tan{(\alpha+\beta)}+\tan{\gamma}}{1-\tan{(\alpha+\beta)}\tan{\gamma}} \\
&=& \displaystyle \frac{\displaystyle \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}}+\tan{\gamma}}{1-\displaystyle \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}}\tan{\gamma}}\\
&=&\displaystyle \frac{\tan{\alpha}+\tan{\beta}+\tan{\gamma}-\tan{\alpha}\tan{\beta}\tan{\gamma}}{1-(\tan{\alpha}\tan{\beta}+\tan{\beta}\tan{\gamma}+\tan{\gamma}\tan{\alpha})}
\end{eqnarray}$$
と、\(\tan{\alpha}\) , \(\tan{\beta}\) , \(\tan{\gamma}\) に関する基本対称式の形でキレイな形が現れます。
ただ、本問を解くだけであれば、実際のところはまず
\(\tan{(\alpha+\beta)}\)
を求めてから処理する方が、計算ミスの可能性は減るでしょう。
これにより、\(\tan{(\alpha+\beta+\gamma)}=1\) と求まります。
一般角で言えば、整数 \(n\) を用いて
\(\alpha+\beta+\gamma=\displaystyle \frac{\pi}{4}+n\pi\)
となります。
今回の \(\alpha+\beta+\gamma\) の範囲を考えてみると、\(\alpha\) , \(\beta\) , \(\gamma\) は \(\displaystyle \frac{\pi}{4}\) よりは大きな鋭角ですから
\(\displaystyle \frac{3\pi}{4} \lt \alpha+\beta+\gamma \lt \displaystyle \frac{3\pi}{2}\)
であり、この範囲では
\(\alpha+\beta+\gamma=\displaystyle \frac{5\pi}{4}\)
を得ることになります。
(3) について
裸の角度に対して、我々はほとんど何もできません。
今回の角度、\(\beta-\alpha\) , \(\gamma-\beta\) は鋭角の範囲ですから、\(\tan{ \ }\) の服を着せることにより
\(\tan{(\beta-\alpha)} \gt \tan{(\gamma-\beta)}\)
を目指しましょう。
(4) について
大まかな路線としては2路線考えられます。
路線1:誘導に乗る
(3) が意味するのは
\(2\beta \gt \alpha+\gamma\)
ということであり、(2) を活かすために両辺 \(\beta\) を加えると
\(3\beta \gt \alpha+\beta+\gamma=\displaystyle \frac{5\pi}{4}\)
すなわち
\(\beta \gt \displaystyle \frac{5\pi}{12}\)
を得ます。
路線2:\(\mathrm{tan}\) の服を着せる
(3) 同様に結局示すべきは
\(\tan{\beta} \gt \tan{\displaystyle \frac{5\pi}{12}}\)
です。
加法定理により、\(\tan{\displaystyle \frac{5\pi}{12}}\) は計算できますから、その値と \(\tan{\beta}\) である \(5\) の値を比較すればよいでしょう。
図形的には
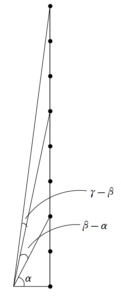
今回の \(\tan{\alpha}=2\) , \(\tan{\beta}=5\) , \(\tan{\gamma}=8\) という状況を一つの図で見てみると

というような状況です。
- この絵で言う \(\displaystyle \frac{5\pi}{12}\) ってどのあたりだろ?
みたいなことを考えると、何が言えればよいのかなども見えやすくなるでしょう。
答案に表立って現れるわけではありませんが、自分の中ではこの図形的なイメージが次の一手を促す補助的な役割になりました。
情報を視覚化したり、視覚化できるかどうかを考える習慣はいざというときに自分を助けてくれます。
解答はコチラ