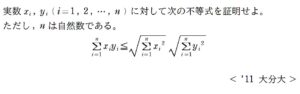問題はこちら(画像をクリックするとPDFファイルで開きます。)

コーシー・シュワルツの不等式と呼ばれる有名不等式です。
今は範囲外ですが、行列という分野の中で「ケーリー・ハミルトンの定理」というものがあります。
参考書によっては「ハミルトン・ケーリーの定理」などとも呼ばれており、呼び方論争もあります。
コーシーシュワルツの不等式はシュワルツ・コーシーの不等式とは呼ばれません。
なぜでしょうか?
品川庄司を庄司品川と呼ばないのと同じ理由だと思います。
さて、どうでもいい話はここまでにして、本題にうつります。
コーシー・シュワルツの不等式は有名不等式であり、
- どこかで見たことある
- 何かの問題で別解として載っていた
というように、何かしらの形で目にしたことはあると思います。
(はじめましてという方は新鮮な気持ちで取り組んでみてください)
その他の有名不等式から派生したりするため、その証明方法は多岐に渡ります。
数ある証明の中でも一番有名な解法を今回は取り上げてみます。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
まず、\(x_{1}=x_{2}=\cdots=x_{n}=0\) のときは等号が成立します。
\(y_{1}=y_{2}=\cdots=y_{n}=0\) のときも同様です。
そこで、それ以外のときを考えてみると、右辺は正の数ということになります。
左辺が負のときは成立するに決まっていますから、左辺が正の数のときを考えれば十分です。
このとき示すべき不等式は
\((\displaystyle \sum_{i=1}^n x_{i}y_{i})^{2} \leq (\displaystyle \sum_{i=1}^n x_{i}^{2})(\displaystyle \sum_{i=1}^n y_{i}^{2})\)
です。
ここで、示すべき不等式の形を見てみましょう。
\(○^{2}-☆△ \leq 0\)
という形から何かをインスピレーションしませんか \(\cdots\) ?
これがインスピレーション出来たら、今後、コーシーシュワルツの不等式は自力で復元できるようになっているはずです。
頑張ってみましょう。
解答はコチラ