問題はこちら(画像をクリックするとPDFファイルで開きます。)
(1) , (2) について
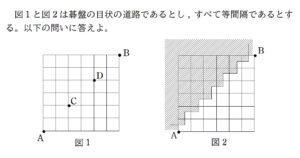
最短経路の問題として (1) , (2) についてはきっちりと確保したいレベルの基本問題です。
(3) について
反面、(3) については「カタラン数」という話題にスポットが当たっており、
経験していなければ、その場での発想は不可能
と言ってもよいと思います。
カタラン数の話題を無視して、「純粋に腕力で押し切る」ということもできますので、試験場では腕力で愚直に計算することもできますが、ここではカタラン数という話題に沿った解法で解いてみたいと思います。
カタラン数については紙面上で説明するのが難しく、一つの図に色々書き込むと「図が五月蝿い」という状態になります。
なので、なるべく図を分けて書いたため、スペースをとってしまいました。
実際の答案では、もう少しコンパクトにまとめれる部分はまとめた方がいいかなと思いますので、そのあたりは各自でお願いします。
カタラン数を扱った整数問題
こちらもCHECK
-

-
カタラン数が素数となるための条件【2021年度 東京工業大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 今回設定されている \(a_{n}=\displaystyle \frac {{}_{2n}\mathrm{C}_n}{n+1}\) ...
続きを見る
経験値が必要な経路問題の難問
併せて解きたい
-

-
蛇経路【経路問題の難問】【1994年度 千葉大学ほか】
例題はこちら(画像をクリックするとPDFファイルで開きます。) 定番の経路問題をベースとして、プラスアルファの思考要素が入った問題です。 (1) は落としたくないレベルですが、(2) は難問です。 東 ...
続きを見る
最短経路の思考系の難問
これも良問
-

-
最短経路と直進距離に関する考察【隣り合わないように並べる方法】【2012年度 高知大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) (1),(2)までは典型的な教科書レベルの問題です。 頭を使うのは(3),(4)からで、5m以上の直進があるような最短距離 ...
続きを見る