問題はこちら(画像をクリックするとPDFファイルで開きます。)
2つの動点が関わる軌跡や通過領域について捉える問題です。
難易度についてははっきりと差が付くと思います。
何が難しいの?と思う人もいるでしょうし、ドツボに嵌まって身動きが取れなくなる人もいると思います。
本問を選定した理由を述べます。
通過領域というのは本来、目で追っていくことが難しいから式に教えてもらおうという態度でいくことが多いです。
そのあたりのよくある通過領域については
【解答速報】2021年度 東京大学理系第1問【放物線の通過領域】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 急ぎで作成したので、誤りや打ち間違いなどがあるかもしれませんが、ご了承ください。 (誤りが発覚し次第、訂正版をアップしていきます。) また、時期が来たら、戦略なども含めた完全版を出したいと思います。 【追記】詳細版に差し替えました。 2021年度東大理系の問題はこちら 本問は「通過領域」がテーマになっています。 速報では逆像法(しらみつぶしの考え方)で倒しました。 放物線が通ることができる点の集合が求める領域です。 \((2 \ ...
問題はこちら(画像をクリックするとPDFファイルで開きます。) 逆像法シリーズ第3講は 通過領域 という難関大入試でも頻出の話題について扱います。 このシリーズの一覧はこちら (以下ネタバレ注意) + クリック(タップ)して続きを読む 直接目で追いきれないので \(\cdots\) 今回、\(a\) が動くにつれて円 \(C_{a}\) も動くわけですが、中心、半径が同時に動くため、ラフな動きはともかく、細かな動きを目で追いきることは難しいでしょう。 そこで、逆に ...
直線の通過領域、線分の通過領域【2009年度 横浜国立大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 難関大頻出の話題である「通過領域」の問題の中でも、一番シンプルな「直線の通過領域」について考えます。 さらに、その延長にある「線分の通過領域」についても扱います。 なお、通過領域に関する根本的な考え方については で扱っていますので、考え方の根っこについて押さえたい人はそちらを参考にしてください。 本問は逆像法のココロはおさえた上で、線分の通過領域というワンパンチあるテーマを考えるということで、「実践演習」の方で扱います。 (以下ネタバレ注意) ...
円の弦の通過領域【2円の交点を結ぶ線分】【1994年度 東京都立大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 円と円の交点を結ぶ線分の通過領域を求める問題です。 円 \(C\) は固定されていますが、円 \(C'\) の動きは点 \((1 \ , \ 0)\) を通りながら動くというパッと見よく分からない動き方をします。 円 \(C'\) の動きは式的にかろうじて追うことができるでしょう。 その動きに伴う共有弦の動きを細かな部分まで目で追いきるとなると限界があるでしょう。 そのあたりをどのように扱うかは、経験がモノをいいます。 通過領域の根本的な考え ...
通過領域【式で追うか目で追うか】【2004年度 青山学院大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 2つの動点が関わる軌跡や通過領域について捉える問題です。 難易度についてははっきりと差が付くと思います。 何が難しいの?と思う人もいるでしょうし、ドツボに嵌まって身動きが取れなくなる人もいると思います。 本問を選定した理由を述べます。 通過領域というのは本来、目で追っていくことが難しいから式に教えてもらおうという態度でいくことが多いです。 そのあたりのよくある通過領域については で、取り扱っています。 最初にいってしまうと、この問題は式だけで ...
問題はこちら(画像をクリックするとPDFファイルで開きます。) 東大お得意の通過領域を絡めた問題で、「動くもの」をどのように数式として立式するかという運用力が求められます。 領域を出すだけでも一苦労なのですが、その後の面積計算においても工夫なしでやろうと思うと少し溜息が出ます。 本問は、上記の運用力に加え、構造を的確にとらえて処理する力を鍛えられると思います。 (以下ネタバレ注意) + クリック(タップ)して続きを読む 構造の把握 いきなりで分からなかった場合、例えば \(k=1\) などと ...
問題はこちら(画像をクリックするとPDFファイルで開きます。) 線分の通過領域をテーマとする難関大では頻出の話題です。 本サイトでも、 などで扱っています。 この話題に対しては、順像法、逆像法、包絡線など、様々な解法があります。 特に逆像法については、考え方が独特であり、ある程度数をこなし慣れていないと中々自分のものにすることが難しいでしょう。 本サイトでは テーマ別演習:逆像法 で扱っており、通過領域に関しては第3講で扱っています。 通過領域は、話題的に難易度は高いですが、難関大においては登場頻度は高く ...
問題はこちら(画像をクリックするとPDFファイルで開きます。) 円を折り返したときの折り目の存在範囲を考える問題です。 シンプルな題意ですが、解き進めていくといくつかの上級テーマが次から次へと襲い掛かってくるため、完答するためにはそれらを払いのけるだけの確固たる力が必要です。 (以下ネタバレ注意) + クリック(タップ)して続きを読む 座標の設定 まずは座標の設定です。 自然に設定するとしたら \(\mathrm{A}\)\((-1 \ , \ 0)\) , \(\mathrm{B}\)\((1 \ , ...
問題はこちら(画像をクリックするとPDFファイルで開きます。) 線分の通過領域による立体の体積を求める問題です。 点 \(\mathrm{P}\) は1次元的な動きですが、点 \(\mathrm{Q}\) は2次元的な動きをします。 同時に動かすと中々想像がつきませんが、ひとまず 点 \(\mathrm{P}\) を固定して \(\mathrm{Q}\) だけ動かす といったように、一つずつ動かすと分かりやすいでしょう。 独立2変数の扱いに通じる部分がありますね。 この態度で考えを進めると、結局は \(\ ...
2024年度 京都大学理系第2問【独立に動く2点を結ぶ線分の中点の存在領域】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 円板上の点と円周上の点を両端にもつ線分の中点の存在領域を考える問題です。 複素数 \(x\) , \(y\) はお互いに干渉することなく、独立に動くため、 まずは片方を固定し、1つずつ動かす という予選決勝法の考え方で捌いていくことを考えます。 その際、先にどちらを固定するかという点で体感のやりやすさ・やりにくさが若干変わってきます。 複素数を複素数のまま扱う方法もありますし、実部・虚部を持ち出し、 \(z=p+qi\) などとおいて、この ...
で、取り扱っています。
最初にいってしまうと、この問題は式だけで押し通そうと思うとツライです。
ある程度目で追っていく部分が必要になってくるわけです。
もちろん、式で追う部分もあり、その切り替える力が必要になるため、いい訓練となる問題かなと思い選定しました。
(以下ネタバレ注意)
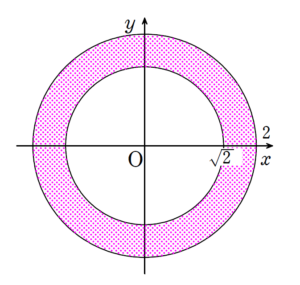
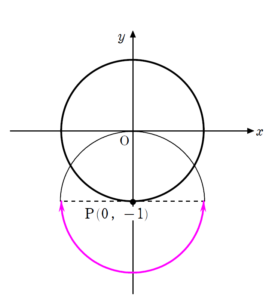
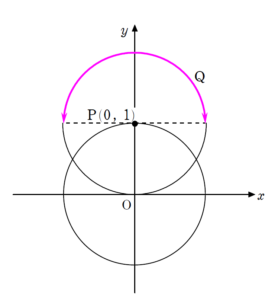
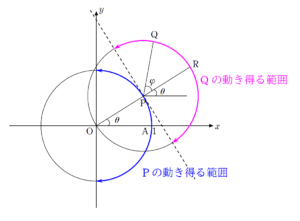
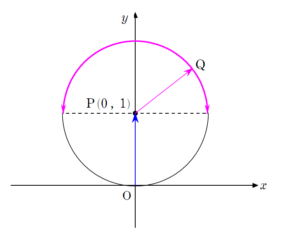
+ クリック(タップ)して続きを読む 与えられた条件 (a) , (b) という状況を図示してみると のようになります。 \(\angle{\mathrm{AOP}}=\theta\) , \(\angle{\mathrm{RPQ}}=\varphi\) と設定すると、 \(\overrightarrow{ \mathrm{OP} }=\left( \(\overrightarrow{ \mathrm{PQ} }=\left( であり、 \(\overrightarrow{ \mathrm{OQ} }=\overrightarrow{ \mathrm{OP} }+\overrightarrow{ \mathrm{PQ} }\) ですから $$\overrightarrow{ \mathrm{OQ} }=\left( と、\(\mathrm{Q}\) の座標は \(\theta\) , \(\varphi\) で表せます。 (1) は \(\theta=\displaystyle \frac{\pi}{2}\) のときを考えることになります。 そうなると結論だけで言えば と見えてしまうかもしれません。 (【解答】ではある程度は記述してあります) (2) は \(\varphi=\displaystyle \frac{\pi}{2}\) , または \(\varphi=-\displaystyle \frac{\pi}{2}\) のときを考えることになります。 \(\varphi=\displaystyle \frac{\pi}{2}\) のとき \(\overrightarrow{ \mathrm{OQ} }=\left( となります。 \(\mathrm{Q}\) の座標を \((X \ , \ Y)\) とおくと $$\begin{eqnarray} ということを意味します。 \(\mathrm{Q}\) の軌跡が欲しいわけですから、ここから \(\theta\) を消去して \(X\) , \(Y\) の関係式を Get しにいくのが自然でしょう。 その際、\(\theta\) の範囲が縛られている以上、\(X\) , \(Y\) もそれに縛られるわけですから、 軌跡の限界(範囲) に注意しましょう。 $$\begin{eqnarray} という一般論で \(\mathrm{Q}\) の動く領域を捉えていくわけです。 式的に攻めようと思うと \(\theta\) , \(\varphi\) を消去して \(X\) , \(Y\) の関係式を Get しにいこうとすると思います。 2文字ありますが、消しやすそうな \(\theta\) を狙って、\(X^{2}+Y^{2}\) を計算してやります。 詳しい計算過程は【戦略】の中でやっていますが \(X^{2}+Y^{2}=2+2\cos{\varphi}\) と得られます。 \(-\displaystyle \frac{\pi}{2} \leq \varphi \leq \displaystyle \frac{\pi}{2}\) ですから \(2 \leq 2+2\cos{\varphi} \leq 4\) となります。 これより \(2 \leq X^{2}+Y^{2} \leq 4\) ですから という円環部分に \((X \ , \ Y)\) が存在することが分かりました。 しかし、\(-\displaystyle \frac{\pi}{2} \leq \theta \leq \displaystyle \frac{\pi}{2}\) をどのように \(X\) , \(Y\) の範囲に結び付ければよいかということを考えると、この辺りで限界を迎えます。 式で攻める路線から、潔く切り替えて目で追っていくことにします。 \(\theta=-\displaystyle \frac{\pi}{2}\) のときの半円 が \(\theta=\displaystyle \frac{\pi}{2}\) のときの状況 となるまでの状況は目で追っていけますね。 要するにピンクの半円の通過領域だと分かれば、 回転の中心からの最大距離と最小距離に注目する という見方をすればよいでしょう。 理系の方であれば、数Ⅲの回転体の体積などでこの考え方を運用する機会が多いと思います。ひとまず状況をかいてみる
\begin{array}{c}
\cos{\theta} \\
\sin{\theta} \\
\end{array}
\right)\)
\begin{array}{c}
\cos{(\theta+\varphi)} \\
\sin{(\theta+\varphi)} \\
\end{array}
\right)\)
\begin{array}{c}
\cos{\theta} \\
\sin{\theta} \\
\end{array}
\right)+\left(
\begin{array}{c}
\cos{(\theta+\varphi)} \\
\sin{(\theta+\varphi)} \\
\end{array}
\right)$$(1) について
(2) について
\begin{array}{c}
\cos{\theta} \\
\sin{\theta} \\
\end{array}
\right)+\left(
\begin{array}{c}
\cos{(\theta+\displaystyle \frac{\pi}{2})} \\
\sin{(\theta+\displaystyle \frac{\pi}{2}}) \\
\end{array}
\right)=\left(
\begin{array}{c}
\cos{\theta}-\sin{\theta} \\
\sin{\theta}+\cos{\theta} \\
\end{array}
\right)\)
\left\{
\begin{array}{l}
X=\cos{\theta}-\sin{\theta} \\
Y=\sin{\theta}+\cos{\theta}
\end{array}
\right.
\end{eqnarray}$$(3) について
\left\{
\begin{array}{l}
X=\cos{\theta}+\cos{(\theta+\varphi)} \\
Y=\sin{\theta}+\sin{(\theta+\varphi)}
\end{array}
\right.
\end{eqnarray}$$