空間座標における回転体【ズレて刺さった団子の回転体】【2014年度 名古屋大学】

問題はこちら（画像をクリックするとPDFファイルで開きます。）

空間座標における回転体というトピックスで、難関大を目指すにあたっては避けては通れない話題です。

一般に

がポイントになる点です。

全体像については「仮に分かったとしても、それが体積を求めることに役に立つのか？」ということを考えれば、考えるだけ無駄です。

むしろ混乱するだけなので、考えない方がいいぐらいです。

例え解き終わっても全体像はよく分かりません。

したがって解く前から悩む必要はありません。

切ってから回しても、回してから切っても、「断面」は同じです。

先に回すということは「先に回して全体像をつかもう」ということを無意識にやっているということです。

何度も言います。本問を解くのに全体像は不要です。

回転の中心からの最大距離と最小距離については、実際に回す際に「取っ手をもって回す」というイメージをもつと理解しやすいと思います。

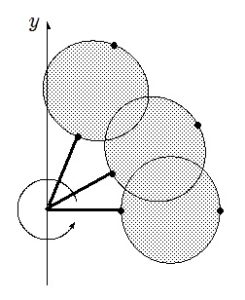
さて、上記の話の内容だけでこの話題をマスターできたら、その人は相当優秀です。

ただ、多くの人は「実際の問題の中でどのように上述の内容が運用されるのか」の方が知りたいのではないでしょうか。

「こうやって泳ぐんだよ」と言われたところで泳げるようにはならないのと同じで、実際に水の中でもがいて要領を掴むものだと思います。

実際の解答の中に上記の内容がどのように息づいているのかも含めて確認をしてみてください。

もちろん受験生の方は解答を見る前に自力で考えることもお忘れなく。

また、数をこなしてこのトピックスの足元を固めたいという人は

も併せて確認してみてください。

解答はコチラ