問題(改作)はこちら(画像をクリックするとPDFファイルで開きます。)
楕円の法線と焦点に関する美しい比率に関する性質の問題です。
原題は次のようでした。
原題はこちら(画像をクリックするとPDFファイルで開きます。)
原題では、(2) で考える特別な点 \(\mathrm{P}\) に関して、
\(\displaystyle \frac {\mathrm{PF_{1}}}{\mathrm{PF_{2}}}=\displaystyle \frac {\mathrm{QF_{1}}}{\mathrm{QF_{2}}}\)
という比率が等しい性質を示させるもので、証明というよりも具体的数値による確認という意味合いが強い問題でした。
それだとあまり面白くないため、より一般化したものの証明として改作をもってきました。
ひとまず改作を解いてみて、重いと感じたら原題の方で要領をつかんでみてください。
(以下ネタバレ注意)
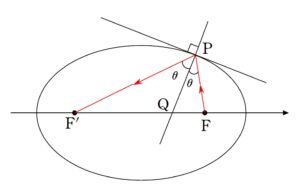
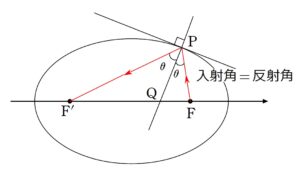
+ クリック(タップ)して続きを読む \(c\) を \(c \gt 0\) なる定数とし、定点 \(\mathrm{F_{1}}\)\((c \ , \ 0)\) , \(\mathrm{F_{2}}\)\((-c \ , \ 0)\) に対し \(\mathrm{PF_{1}}+\mathrm{PF_{2}}=(一定値)\) となるような点 \(\mathrm{P}\) の軌跡が表す曲線 というのが楕円の定義です。 この「一定値」を \(a\) とおいてもいいのですが、\(2a\) としておくと、後の計算が楽になります。 そこで \(\mathrm{PF_{1}}+\mathrm{PF_{2}}=2a\) を満たす点 \(\mathrm{P}\) \((X \ , \ Y)\) の軌跡について考えます。 \(\sqrt{(X-c)^{2}+Y^{2}}+\sqrt{(X+c)^{2}+Y^{2}}=2a\) ですから、 \(\sqrt{(X-c)^{2}+Y^{2}}=2a-\sqrt{(X+c)^{2}+Y^{2}}\) であり、 \((X-c)^{2}+Y^{2}=4a^{2}-4a\sqrt{(X+c)^{2}+Y^{2}}+(X+c)^{2}+Y^{2}\) となります。 これを整理すると \(a^{2}+cX=a\sqrt{(X+c)^{2}+Y^{2}}\) 再び2乗すれば \((a^{2}+cX)^{2}=a^{2}\{(X+c)^{2}+Y^{2}\}\) これを整理すると \((a^{2}-c^{2})X^{2}+a^{2}Y^{2}=a^{2}(a^{2}-c^{2})\) これより、 \(\displaystyle \frac {X^{2}}{a^{2}}+\displaystyle \frac {Y^{2}}{a^{2}-c^{2}}=1\) を得ます。 結局この形は \(\displaystyle \frac {X^{2}}{定数}+\displaystyle \frac {Y^{2}}{定数}=1\) という形であり、見栄えを整えるために \(a^{2}-c^{2}=b^{2}\) とおくことで \(\displaystyle \frac {X^{2}}{a^{2}}+\displaystyle \frac {Y^{2}}{b^{2}}=1\) という形を得るわけです。 今は一般的に処理しましたが、改作の (1) は \(c=1\) のときです。 要領は同じで、 ということを根気よく繰り返し、根号を消していくという作業です。 法線を出そうと思うと、その前に接線の傾きが必要です。 楕円の接線公式を用いてもよいですし、ここではより根本的に微分を用いて接線の傾きを求めます。 それさえできれば、法線の傾きが Get できるため、法線の方程式が求まり、\(x\) 軸との交点 \(\mathrm{Q}\) の座標も求まります。 これにより、 \(\mathrm{PF_{1}}\) , \(\mathrm{PF_{2}}\) , \(\mathrm{QF_{1}}\) , \(\mathrm{QF_{2}}\) が全て立式できます。 本問の結果は 光学的性質 楕円を鏡と思ったとき、 という楕円の光学的性質の証明となっています。 本問の結果から、 \(\displaystyle \frac{\mathrm{PF'}}{\mathrm{PF}}=\displaystyle \frac{\mathrm{QF'}}{\mathrm{QF}}\) が言えるため、点 \(\mathrm{P}\) における法線は \(\angle{\mathrm{FPF'}}\) の二等分線 ということになります。 このとき、 \(\angle{\mathrm{FPQ}}=\angle{\mathrm{F'PQ}}={\theta}\) とおきます。 そうなると、 入射角と反射角が等しい すなわち完全反射が起こっていることを意味します。 本問は第1象限の点 \(\mathrm{P}\) についてのみ考えましたが、対称性から楕円上の任意の点でこの現象が起こっています。 注意
接線の傾きがない場合でも、明らかに焦点で反射した光は、もう一方の焦点に向かいます。 法線の傾きがない場合、すなわち、法線が \(y\) 軸である場合でも、明らかにこの法線 ( \(y\) 軸 ) は \(\angle{\mathrm{FPF'}}\) の二等分線 ですから、 \(\displaystyle \frac{\mathrm{PF'}}{\mathrm{PF}}=\displaystyle \frac{\mathrm{QF'}}{\mathrm{QF}}\) が言えるため、完全反射が起こっています。 改作の方は、問題文的に曲線 \(C\) が楕円であることは前提とせず、純粋に \(\mathrm{PF_{1}}+\mathrm{PF_{2}}=2a\) という性質のみを頼りにして方程式を導くという態度としましたが、原題では、楕円の方程式が \(\displaystyle \frac{x^{2}}{a^{2}}+\displaystyle \frac{y^{2}}{b^{2}}=1\) と与えられることを前提とした解答としておきます。 原題での【総括】の後に、楕円についての定義や接線公式についてまとめておきましたので、曖昧に記憶のみを頼りにしていたという人は根本理解のために一読してみてください。 なお、楕円の光学的性質について扱った問題として 問題はこちら(画像をクリックするとPDFファイルで開きます。) 有名な2次曲線の性質の問題です。 背景には「楕円と双曲線の光学的性質」があります。 楕円の光学的性質 \(F ... 続きを見る も参考にしてみてください。問題(改作)はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
楕円の幾何的な定義
(2) について
本問の結果が意味すること
理由
原題について
原題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

参考焦点を共有する楕円と双曲線の性質【楕円と双曲線の光学的性質】【2007年度 北海道大学】


