発想の方向性
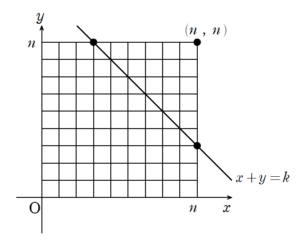
\(x\) 座標と \(y\) 座標の和が \(k\) という状況、すなわち
\((x \ , \ y)\) が、直線 \(x+y=k\) 上
という状況を意味します。
最短経路の問題において

というような斜めのラインがあり、
ということが言えます。
最短経路の問題を何題か経験していれば、この発想は一度は目にしたことがあると思います。
先ほどの
\((x \ , \ y)\) が、直線 \(x+y=k\) 上
という状況も考えると、ますます斜めラインである直線 \(x+y=k\) に目が行くでしょう。
(1) について
\(k=0 \ , \ 1 \ , \ 2 \ , \ \cdots \ , \ 2n\) に対して、最短経路 \(\mathrm{P}\) の通る直線 \(x+y=k\) 上の格子点を
\((x_{k} \ , \ y_{k})\)
とします。
すると、題意の和は
\(\displaystyle \sum_{k=0}^{2n}(x_{k}+y_{k})\)
です。
もちろん、\((x_{k} \ , \ y_{k})\) は直線 \(x+y=k\) 上の点ですから
\(x_{k}+y_{k}=k\)
ということが言え、
$$\begin{eqnarray}
\displaystyle \sum_{k=0}^{2n}(x_{k}+y_{k})&=& \displaystyle \sum_{k=0}^{2n}k \\
&=& \displaystyle \frac{2n(2n+1)}{2}\\
&=&n(2n+1)
\end{eqnarray}$$
と、確かに与えられた \(n\) にのみ依存し、経路に依らない一定値となることが言えました。
(2) について
今度は題意の和は
\(\displaystyle \sum_{k=0}^{2n}({x_{k}}^{2}+{y_{k}}^{2})\)
です。
もちろん
\(x_{k}+y_{k}=k\)
と結びつけるために
$$\begin{eqnarray}
{x_{k}}^{2}+{y_{k}}^{2}&=& (x_{k}+y_{k})^{2}-2x_{k}y_{k} \\
&=& k^{2}-2x_{k}y_{k}
\end{eqnarray}$$
と見たいところです。
これにより、\({x_{k}}^{2}+{y_{k}}^{2}\) が最大のときを考えたければ
- \(x_{k}y_{k}\) が最小となるときを考えればよい。
ということになります。
\(x+y=k\) 上の格子点
\((0 \ , \ k)\) , \((1 \ , \ k-1)\) , \(\cdots\) , \((k-1 \ , \ 1)\) , \((k \ , \ 0)\)
に対し、\(x\) 座標と \(y\) 座標の積の最小値は \(0\) ということは感覚的に分かります。
つまり、正方形の周上を通って \((n \ , \ n)\) まで行く経路が求めるものなのかという予想は立ちます。
ただ、\(k=n+1 \ , \ n+2 \ , \ \cdots \ , \ 2n\) のときは

というように、
\((0 \ , \ k)\) , \((k \ , \ 0)\) が \(x+y=k\) 上に入ってきません。
このあたりでケチをつけられないようにどのように乗り越えるかという部分が頭を使う所でしょう。
ここから先は思考力の範疇です。
\(x_{k}+y_{k}=k\) という関係式を活かそうということを考えてみましょう。
解答はコチラ