問題はこちら(画像をクリックするとPDFファイルで開きます。)
複素数の見た目をしており、確かに前半は1の3乗根の基本性質の運用がメインの話題です。
(1) の結論を得て、(2) に取り掛かる際に「ムムっ」となる可能性があります。
範囲的にはグレーゾーンかもしれませんが、余裕があればこういう問題も考えて見るのも一興です。
(以下ネタバレ注意)
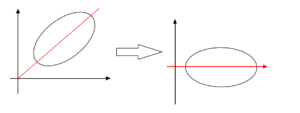
+ クリック(タップ)して続きを読む \(|z|=1\) という条件から、\(|z|^{2}=1\) ですから、 \(z\bar{z}=1\) として処理します。 これより \((x\omega+y{\omega}^{2})(x\bar{\omega}+y{\bar{\omega}}^{2})=1\) を処理することになります。 という1の虚数立方根の性質を駆使しながら、進めていく路線が見えると思います。 \((x\omega+y{\omega}^{2})(x\bar{\omega}+y{\bar{\omega}}^{2})=1\) を展開して整理すると \(x^{2}\omega \bar{\omega}+xy\omega \bar{\omega}(\omega+\bar{\omega})+y^{2}{\omega}^{2}{\bar{\omega}}^{2}=1\) となり、\(\omega\) の上記性質から ですから、結局 \(x^{2}-xy+y^{2}=1\) という結論を得ます。 これが曲線 \(C\) の表す方程式です。 \(x^{2}-xy+y^{2}=1\) という方程式が表す図形を初見で看破できる方がいたら、それは素晴らしいです。 ただ、多くの人にとっては初見だと 「あれ?どっかで計算ミスった?」 と慌てふためくことになります。(むしろ健全な反応) 切り崩すためには観察力が必要です。 ということが看破できれば 点 \((a \ , \ b)\) が \(C\) 上ならば、\((b \ , \ a)\) も \(C\) 上の点である ということが分かり、これは ということを意味します。 ここまで晒しても「だから何だよ」と思うか、「あ、そうか」と思うか分かれると思います。 \(y=x\) について対称であるということは というように ということです。 そうなってくると、\((x \ , \ y)\) を \(-\displaystyle \frac{\pi}{4}\) 回転させた点を \((X \ , \ Y)\) と設定し、 \(X\) , \(Y\) の関係式を Get したい と思えてくるはずです。 ここまでくれば後は手なりに進んでいくはずです。(1) について
(2) について