問題はこちら(画像をクリックするとPDFファイルで開きます。)

完全順列、攪乱順列、モンモール数などと呼ばれる話題の問題で、1994年度慶応大、2004年度東工大など類題も多く見られます。
本問のように \(5\) 人といったような具体的な場合であれば、樹形図をかき、腕力で押し切ることも可能でしょう。
(ただ、工夫しないとそれなりの大木になるでしょう。)
ただ、ここでは一般的な \(n\) のときでも話が通じる態度である漸化式を立てる方針で考えてみます。
完全順列に対する漸化式の立て方は独特なものがあります。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
完全順列とは
\(1\) 番から \(n\) 番までの番号がついた球と箱が1つずつあるとします。
これらの球を左から並べて箱に一つずつ入れていくことを考えます。
このとき、箱の番号と球の番号が一致しないような並べ方を完全順列と言います。
もう少し順列っぽい言い方をすると
\(1\) から \(n\) の数字を \(1\) 列に並べた順列のうち、\(k=1 \ , \ 2 \ , \cdots \ , \ n\) に対して
どの \(k\) 番目の数も \(k\) ではないもの
という言い方になるでしょうか。
本問もアルファベットよりも数字の方が記述がしやすいので、人に \(1\) , \(2\) , \(\cdots\) とゼッケンをつけ、プレゼントを入れる箱にも \(1\) , \(2\) , \(\cdots\) と番号をつけておきます。
- \(1\) 番のプレゼントが \(1\) 番の箱に入らない
- \(2\) 番のプレゼントが \(2\) 番の箱に入らない
\( \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\)
- \(n\) 番のプレゼントが \(n\) 番の箱に入らない
という入れ方を考えるわけです。
このような箱への入れ方を \(a_{n}\) 通りとします。
\(a_{n+2}\) について
完全順列における漸化式の立て方は独特です。
今回のプレゼント交換を例に表現すると
\(1\) 番の人と、\(k\) 番の人のプレゼント交換が成立するか否か
という観点で場合分けをします。
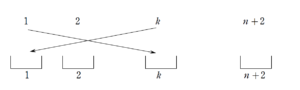
\(1\) 番の人と、\(k\) 番の人のプレゼント交換が成立するとき

\(k\) の選び方は \(n+1\) 通りです。
このとき、残りの \(n\) 人に関するプレゼント交換の仕方は \(a_{n}\) 通りあります。
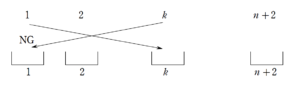
\(1\) 番の人と、\(k\) 番の人のプレゼント交換が成立しないとき

\(k\) の選び方は先ほど同様 \(n+1\) 通りです。
このとき
- \(2\) 番のプレゼントは \(2\) 番の箱に入れられない
- \(3\) 番のプレゼントは \(3\) 番の箱に入れられない
\( \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\)
- \(k\) 番のプレゼントは \(1\) 番の箱に入れられない
\( \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\)
- \(n+2\) 番のプレゼントは \(n+2\) 番の箱に入れられない
と、\(n+1\) 個のプレゼントに対して \(n+1\) 個の「 NG 箱」があるということで
\(a_{n+1}\) 通りの入れ方
となります。
\(n\) が十分大きいとき
\(\displaystyle \frac{a_{n}}{n!}\) は \(n\) 人でプレゼント交換をしたときに、自分の持ってきたプレゼントに当たってしまう「可哀そうな人」が一人もいない確率です。
\(\displaystyle \lim_{n \to \infty}\displaystyle \frac{a_{n}}{n!}\) を計算すると
\(\displaystyle \lim_{n \to \infty}\displaystyle \frac{a_{n}}{n!}=\displaystyle \frac{1}{e}\)
と約 \(36.7\) %ほどです。
\(n\) が十分大きければ、可哀そうな人が一人ぐらいいそうなものなので、極限が \(0\) とならないのは不思議です。
このあたりの計算については【総括】後の【補足】で触れてあります。
解答はコチラ